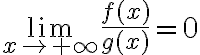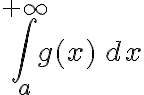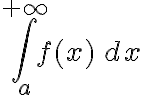Buenas,
Tengo la duda de si el criterio de equivalentes para integrales impropias clasifica cuando el límite de f/g es igual a cero, como lo hace el criterio para series. Esto es lo que está en las notas:

Pienso que sí porque si eso pasa, entonces f tiende a cero más rápido que g y a partir de cierto valor es más chica que g, entonces puedo usar el criterio de comparación y si la integral de g converge, entonces la integral de f también. Pero como no está en la proposición me queda la duda.
Gracias!