Foro Práctico 4

Hola. La desigualdad 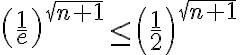$\displaystyle \left(\frac{1}{e}\right)^{\sqrt{n+1}} \leq \left(\frac{1}{2}\right)^{\sqrt{n+1}}$ es cierta, porque 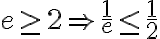$e\geq 2 \Rightarrow \frac{1}{e} \leq \frac{1}{2}$. Igual, ojo con el cambio de variable que decís, porque si llamás 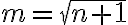$m=\sqrt{n+1}$ entonces 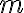$m$ no necesariamente es natural, y no tenemos herramientas para clasificar sumas de cosas cuya variable no es natural. Tendrías que buscar otro argumento para probar que la serie de 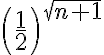$\left(\frac{1}{2}\right)^{\sqrt{n+1}}$ converge.

Saludos