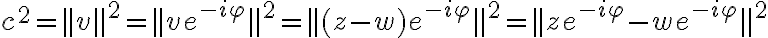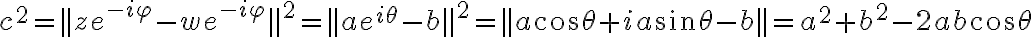Foro de Ejercicios fuera de los Prácticos

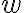Hola. Un posible dibujo para $z$ y $w$ es:

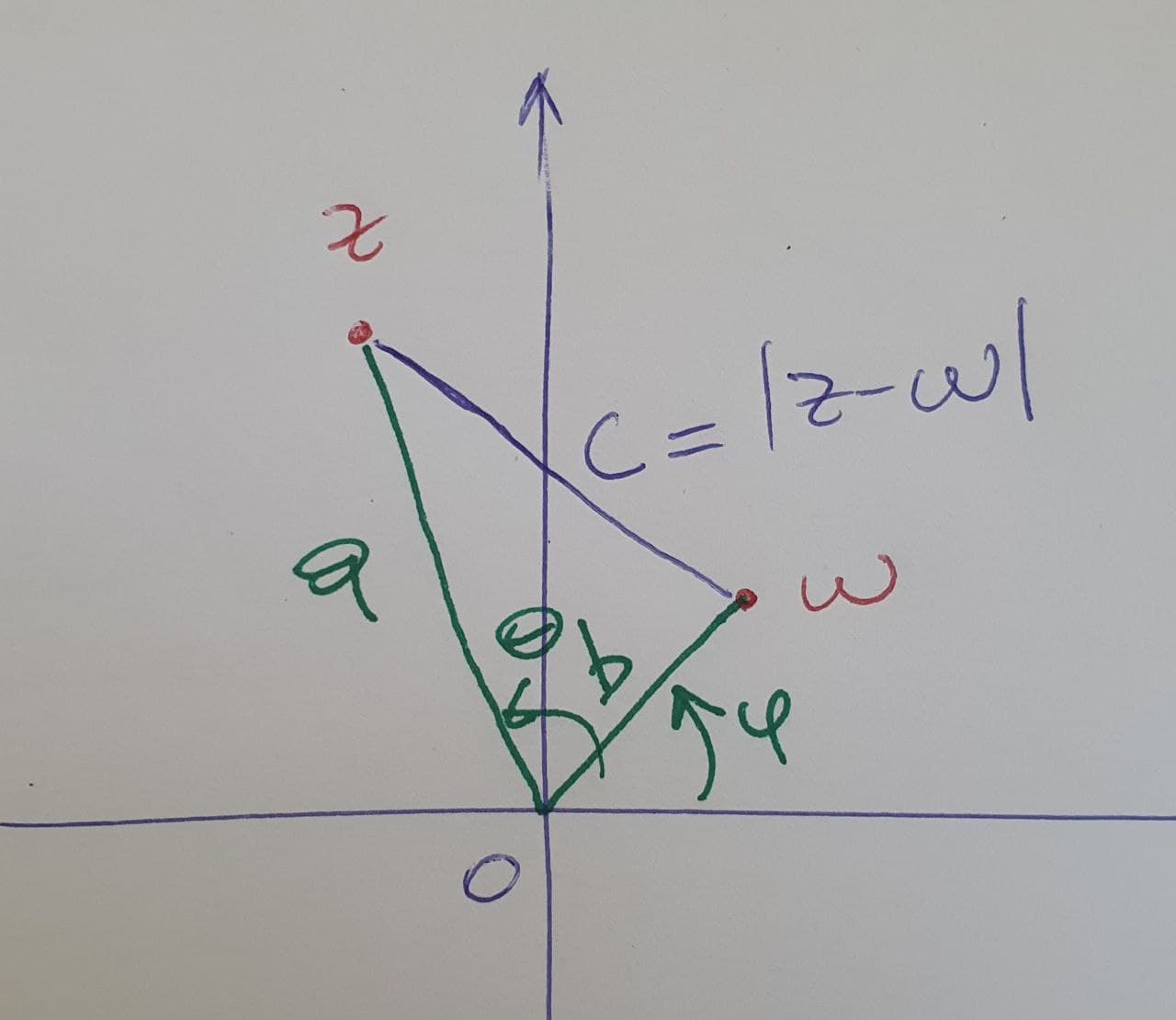
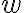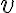Fijate que ese dibujo podés rotarlo para que $w$ quede en el eje $x$ y la distancia $c$ va a seguir siendo igual. Formalmente, si llamás $v$ al complejo 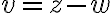$v=z-w$, entonces el complejo 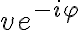$ve^{-i\varphi}$ tiene módulo 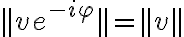$||ve^{-i\varphi}|| =||v||$. Acordate que multiplicar por 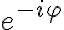$e^{-i\varphi}$ equivale a rotar un ángulo 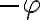$-\varphi$, por lo que al multiplicar por esa cantidad el dibujo queda:

Entonces, tenemos que

$c^2=||v||^2=||ve^{-i\varphi}||^2=||(z-w)e^{-i\varphi}||^2 = ||ze^{-i\varphi} - we^{-i\varphi}||^2$

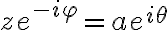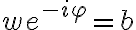Fijate que $ze^{-i\varphi} = ae^{i\theta}$ y que $we^{-i\varphi} = b$, por lo que:

$c^2=||ze^{-i\varphi} - we^{-i\varphi}||^2 =||ae^{i\theta}-b||^2 = ||a\cos\theta + ia\sin\theta -b ||=a^2+b^2-2ab\cos\theta$.

Saludos