Hola. Mi recomendación es que calcules esa área como el área limitada por la elipse menos el área limitada por la circunferencia de radio 2, como en el dibujo:
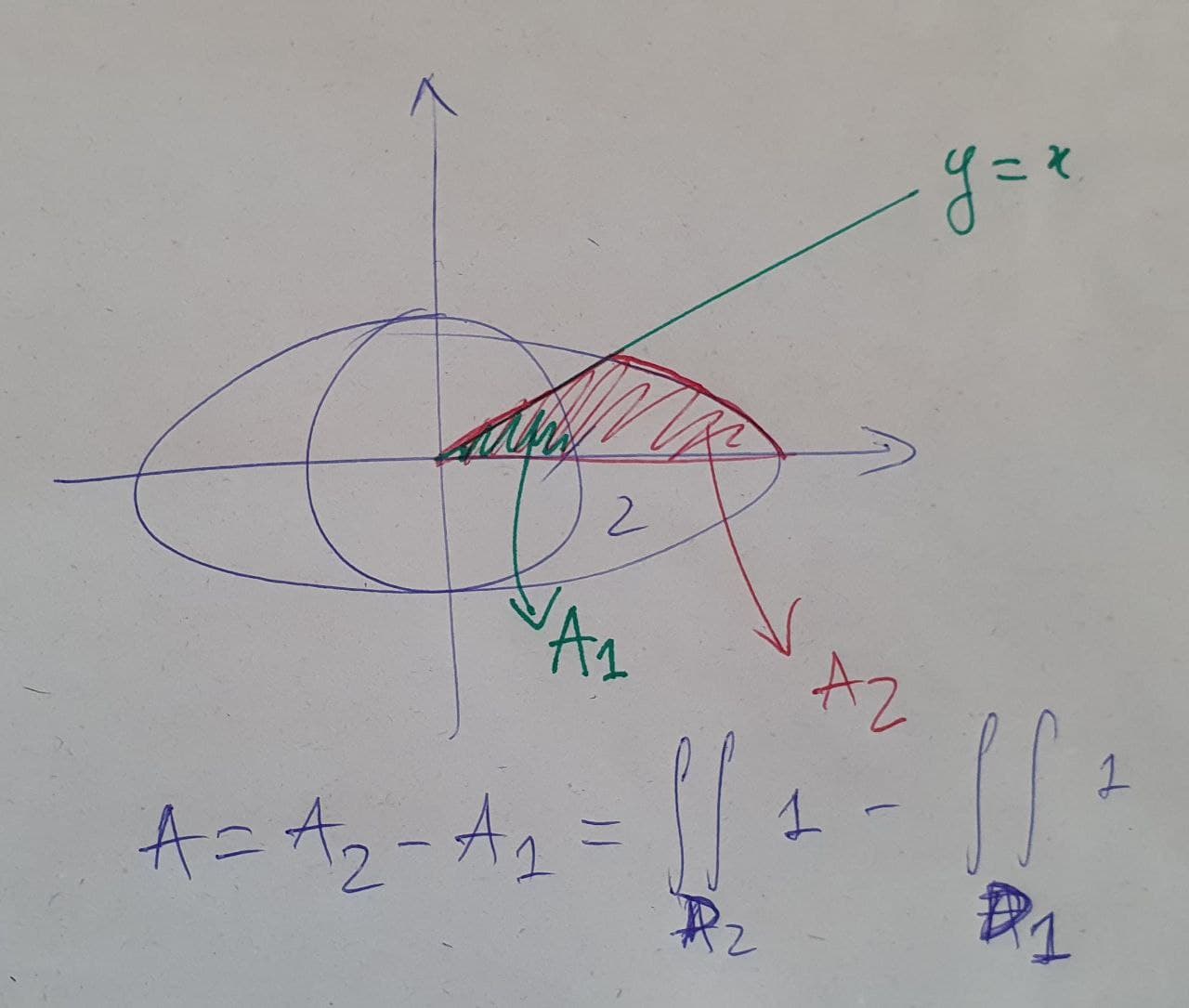
Ahí 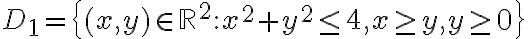 y
y 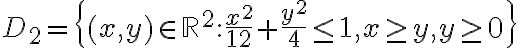 . Para la región
. Para la región 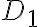 hacés el cambio usual a polares. Fijate que
eso hace que
hacés el cambio usual a polares. Fijate que
eso hace que 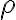 tenga que variar entre
tenga que variar entre  y
y 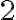 , mientras que la condición
, mientras que la condición 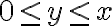 implica que
implica que ![0 \leq \rho\sin\theta \leq \rho\cos\theta \Rightarrow 0 \leq \sin\theta \leq \cos\theta \Rightarrow 0\leq \tan\theta \leq 1 \Rightarrow \theta \in [0,\pi/4] 0 \leq \rho\sin\theta \leq \rho\cos\theta \Rightarrow 0 \leq \sin\theta \leq \cos\theta \Rightarrow 0\leq \tan\theta \leq 1 \Rightarrow \theta \in [0,\pi/4]](https://eva.fing.edu.uy/filter/tex/pix.php/7e944d95bedf99de9c7169a018461089.gif) .
Eso era obvio del dibujo, pero sirve para que veas por qué te dan el dato de la tangente. Para
.
Eso era obvio del dibujo, pero sirve para que veas por qué te dan el dato de la tangente. Para 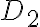 vas a tener que hacer el cambio a polares adaptada a la elipse, y ahí vas a llegar a que la condición
vas a tener que hacer el cambio a polares adaptada a la elipse, y ahí vas a llegar a que la condición 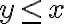 es equivalente a que
es equivalente a que 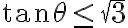 (por eso aparece ese otro dato).
(por eso aparece ese otro dato).
Saludos
