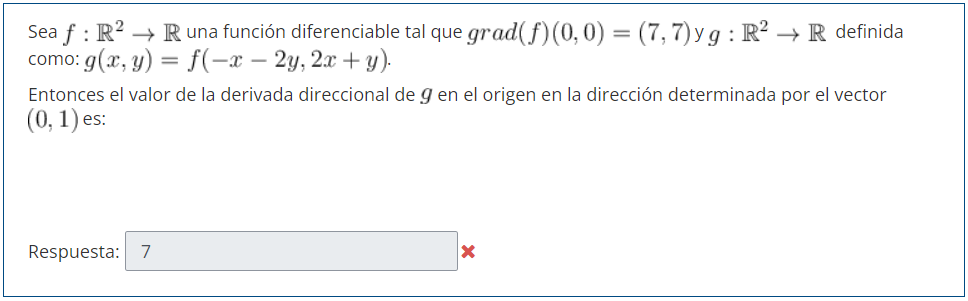
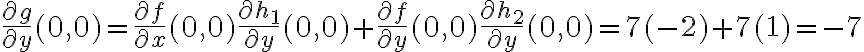Buenas! No he podido con estos ejercicios. El primero lo pude razonar pero no logro relacionar los datos para llegar a un resultado. Y en el segundo llegue a un resultado pero no es el correcto, lo razoné por el lado de que sé el valor de las derivadas parciales de f en (0,0), y g(0,0) es igual a f(0,0), por lo tanto puedo encontrar la derivada parcial en y de g en ese punto (la respuesta correcta es -7). No se si está bien.
Agradezco si alguien puede guiarme. Saludos.