Hola, tu función es 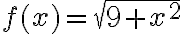 . Lo podés ver como una composición
. Lo podés ver como una composición 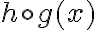 , siendo
, siendo 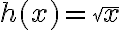 y
y 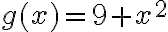 . Por la regla de la cadena
. Por la regla de la cadena 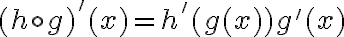 .
.
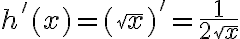 y por lo tanto
y por lo tanto 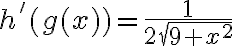 . Por otro lado la derivada de
. Por otro lado la derivada de  es
es 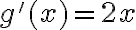 .
.
En definitiva,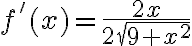 . Evaluás en
. Evaluás en 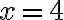 y te da
y te da 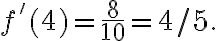
Por otro lado observá que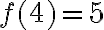 .
.
La recta tangente al gráfico en un punto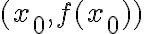 tiene ecuación
tiene ecuación  . Tenés que sustituir
. Tenés que sustituir 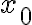 por
por 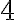 y obtenés la solución.
y obtenés la solución.
Saludos.
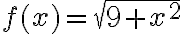 . Lo podés ver como una composición
. Lo podés ver como una composición 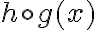 , siendo
, siendo 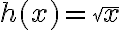 y
y 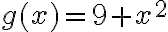 . Por la regla de la cadena
. Por la regla de la cadena 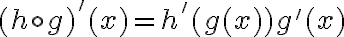 .
. 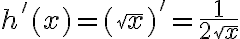 y por lo tanto
y por lo tanto 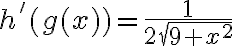 . Por otro lado la derivada de
. Por otro lado la derivada de  es
es 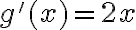 .
.En definitiva,
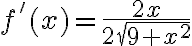 . Evaluás en
. Evaluás en 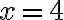 y te da
y te da 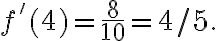
Por otro lado observá que
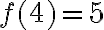 .
. La recta tangente al gráfico en un punto
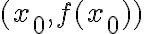 tiene ecuación
tiene ecuación  . Tenés que sustituir
. Tenés que sustituir 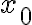 por
por 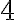 y obtenés la solución.
y obtenés la solución.Saludos.
