Hola. El primer ejercicio lo hicimos en esta clase de consulta. Y para el segundo tenés que aplicar la regla de la cadena:  es la composición de
es la composición de  con la función
con la función 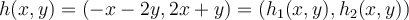 . Por lo tanto, la derivada de
. Por lo tanto, la derivada de  respecto a
respecto a  en
en 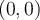 es:
es:
Saludos
Hola. El primer ejercicio lo hicimos en esta clase de consulta. Y para el segundo tenés que aplicar la regla de la cadena:  es la composición de
es la composición de  con la función
con la función 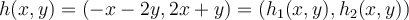 . Por lo tanto, la derivada de
. Por lo tanto, la derivada de  respecto a
respecto a  en
en 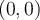 es:
es:
Saludos