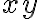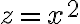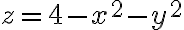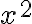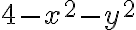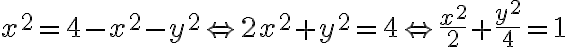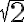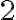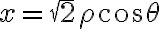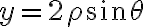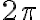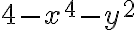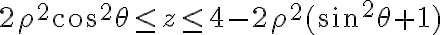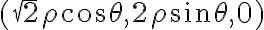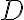Hola. Creo que el problema es que al plantear que en cilíndricas el 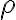 varía entre 0 y 2 lo que estás haciendo es parametrizar una circunferencia de radio 2 (es decir, el par
varía entre 0 y 2 lo que estás haciendo es parametrizar una circunferencia de radio 2 (es decir, el par 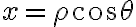 ,
, 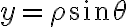 con
con ![\rho \in [0,2] \rho \in [0,2]](https://eva.fing.edu.uy/filter/tex/pix.php/2fa89c7a65caf950705e416d9a656b73.gif) ,
, ![\theta
\in [0,2\pi] \theta
\in [0,2\pi]](https://eva.fing.edu.uy/filter/tex/pix.php/1b6956d2d1568a93d1bce9e42e05fc78.gif) cubre una circunferencia de radio 2 en el plano
cubre una circunferencia de radio 2 en el plano 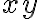 ). Fijate que, si te olvidás de la coordenada
). Fijate que, si te olvidás de la coordenada  , la intersección entre
, la intersección entre 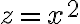 y
y 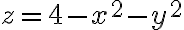 es una elipse, no una circunferencia. Eso podés verlo igualando ambas expresiones:
si
es una elipse, no una circunferencia. Eso podés verlo igualando ambas expresiones:
si  tiene que ser igual a
tiene que ser igual a 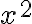 y a
y a 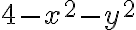 , ambas curvas se van a cortar en los puntos cuyas coordenadas
, ambas curvas se van a cortar en los puntos cuyas coordenadas  e
e  cumplan que
cumplan que
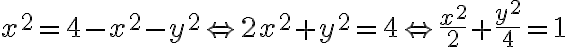
Eso último es la ecuación de una elipse de centro  y ejes
y ejes 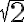 en
en  y
y 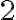 en
en  . Hice un dibujo en Geogebra de estas superficies que tal vez te ayude, está acá:
. Hice un dibujo en Geogebra de estas superficies que tal vez te ayude, está acá:
https://www.geogebra.org/m/adber8cu
Si ponés el dibujo en la perspectiva vertical ("olvidándote" de la dimensión  ), podés confirmar que esas cosas efectivamente se cortan en una elipse en
), podés confirmar que esas cosas efectivamente se cortan en una elipse en 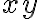 .
.
Por lo tanto, mi sugerencia es que uses cilíndricas "adaptadas" a esa elipse, es decir, 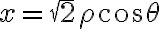 ,
, 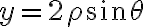 . Con ese cambio de coordenadas,
. Con ese cambio de coordenadas, 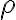 varía entre 0 y 1,
varía entre 0 y 1,  entre 0 y
entre 0 y 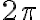 .
.  va a variar
entre
va a variar
entre 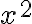 y
y 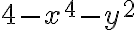 , que con ese cambio de coordenadas resulta
, que con ese cambio de coordenadas resulta 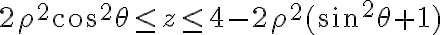 . En el dibujo de Geogebra podés mover las barras de la izquierda que se llaman r y theta. El punto A
del dibujo marca el punto de coordenadas
. En el dibujo de Geogebra podés mover las barras de la izquierda que se llaman r y theta. El punto A
del dibujo marca el punto de coordenadas 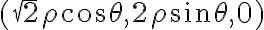 (es decir, el punto de la elipse en el piso). El punto
(es decir, el punto de la elipse en el piso). El punto  es el punto correspondiente en la superficie
es el punto correspondiente en la superficie 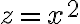 , mientras que el C es el que corresponde
a
, mientras que el C es el que corresponde
a 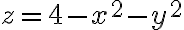 . Me parece que el dibujo te puede ayudar a convencerte que esas restricciones sobre dónde se pueden mover
. Me parece que el dibujo te puede ayudar a convencerte que esas restricciones sobre dónde se pueden mover  ,
,  y
y  (es decir, que
(es decir, que  e
e  se mueven en la elipse y
se mueven en la elipse y  se mueve entre
se mueve entre 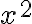 y
y 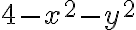 ) efectivamente
hacen que recorras el conjunto
) efectivamente
hacen que recorras el conjunto 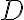 al que le querés calcular el volumen. Si eso te convence, calculando la integral con ese cambio de coordenadas (y acordándote de multiplicar por el determinante del jacobiano del cambio de variable!) deberías llegar
al resultado de la solución.
al que le querés calcular el volumen. Si eso te convence, calculando la integral con ese cambio de coordenadas (y acordándote de multiplicar por el determinante del jacobiano del cambio de variable!) deberías llegar
al resultado de la solución.
En el canal de YouTube del curso está subida una clase de Alejandro Bellati del año pasado donde se hace este ejercicio. Capaz que mirarlo te ayuda.
Saludos

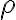
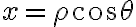
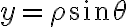
![\rho \in [0,2] \rho \in [0,2]](https://eva.fing.edu.uy/filter/tex/pix.php/2fa89c7a65caf950705e416d9a656b73.gif)
![\theta
\in [0,2\pi] \theta
\in [0,2\pi]](https://eva.fing.edu.uy/filter/tex/pix.php/1b6956d2d1568a93d1bce9e42e05fc78.gif)