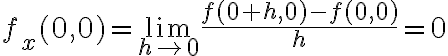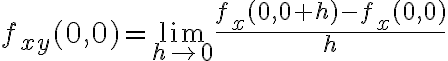Hola. Calcular 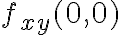 es calcular la derivada parcial respecto a
es calcular la derivada parcial respecto a  en
en  de la función
de la función 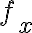 , la derivada parcial de
, la derivada parcial de  respecto a
respecto a  (análogamente para
(análogamente para  ). Para
). Para 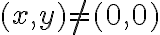 la función
la función 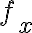 puede calcularse simplemente derivando respecto a
puede calcularse simplemente derivando respecto a  a
a  en ese dominio (es decir, derivando respecto a
en ese dominio (es decir, derivando respecto a  la expresión
la expresión 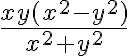 ). Para el
). Para el  la derivada parcial se calcula con el cociente incremental en la dirección
la derivada parcial se calcula con el cociente incremental en la dirección  :
:
Ese límite es 0 ya que 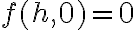 para todo
para todo  . Una vez que tenés la expresión de
. Una vez que tenés la expresión de 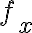 , podés calcular la derivada parcial respecto a
, podés calcular la derivada parcial respecto a  en
en 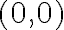 planteando el cociente incremental en la dirección
planteando el cociente incremental en la dirección  de
de 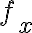 :
:
Haciendo lo mismo con 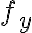 se calcula la otra derivada parcial.
se calcula la otra derivada parcial.
Saludos