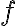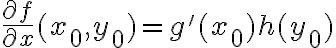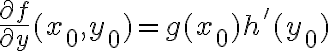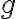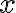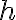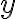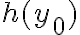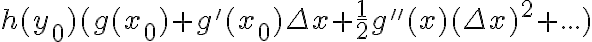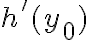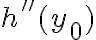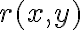Foro Práctico 9

Buenas noches, Ivana.

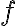
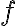
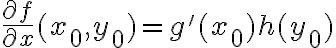
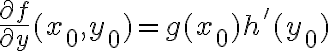
Para la parte a), calculá los primeros términos del polinomio de Taylor de $f$ (hasta el grado tres más o menos, si te ayuda, capaz alguno más). Fijate que estos van a ser relativamente sencillos, ya que las derivadas parciales de $f$ son $\frac{\partial f}{\partial x}(x_0,y_0)=g'(x_0)h(y_0)$ y $\frac{\partial f}{\partial y}(x_0,y_0)=g(x_0)h'(y_0)$. 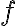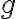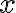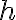Seguís así y te das cuenta que una derivada de orden superior de $f$ es la derivada de $g$ de orden tantas veces como derives según $x$ por la derivada de $h$ de orden tantas veces como derives según $y$. 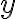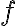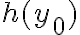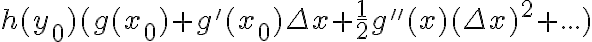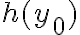Una vez que tengas el polinomio de Taylor de $f$, agrupá los términos que sean múltiplos de $h(y_0)$, sacá este de factor común y te va a quedar $h(y_0)(g(x_0)+g'(x_0)\Delta x+\frac{1}{2}g''(x)(\Delta x)^2+...)$, que es exactamente $h(y_0)$ por el polinomio de Taylor de $g$.
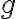
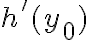
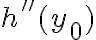
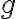
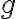
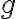
Hacé lo mismo con $h'(y_0)$, con $h''(y_0)$...y vas a ver que lo que te queda dentro del paréntesis de cada término es bastante parecido al polinomio de Taylor de $g$. Intentá sacar cosas de factor común en cada uno para que adentro de quede el polinomio de Taylor de $g$. Al final, terminás viendo que eso que escribiste es el polinomio de Taylor de $g$ por el de $h$.

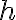
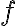
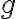
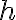
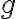
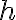
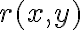
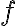
Sobre lo de si el polinomio es de grado infinito, podés hacer esta misma cuenta con el desarrollo de Taylor de orden $n$ de $f$ (que te termina quedando el polinomio de $g$ de orden $n$ por el polinomio de $h$ de orden $n$) teniendo cuidado en cómo acomodar los restos de $g$ y $h$ y para que estos terminen coincidiendo con el resto $r(x,y)$ de $f$, usando que este tiende a cero más rápido que $\|(x,y)\|^n$, 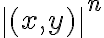o podés hacer la cuenta como si se tratara de la serie de Taylor de $f$ (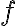el que llamaste de grado infinito) y ver que te queda la serie de Taylor de $g$ por la de $h$.

Para la parte b), procedés de manera similar usando la regla de la cadena.

Saludos.