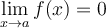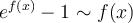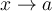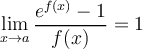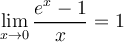Equivalente

Equivalente

de Thiago Caetano Acuña Vinoles -
Número de respuestas: 2

Buenas! Tengo una duda que me surgió haciendo el práctico.

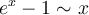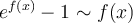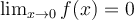Muchas veces he usado la equivalencia: e^x-1 \sim x cerca de 0. Esto viene de la derivada. Sin embargo muchas veces también he usado que   e^{f(x)} -1 \sim f(x) si  \lim_{x\rightarrow 0} f(x) = 0 pero ahora me entra la duda si esto se cumple para cualquier función que tienda a 0 en 0.
En respuesta a Thiago Caetano Acuña Vinoles

Re: Equivalente

de Bernardo Marenco -

Hola. La afirmación es cierta para cualquier función f que tienda a 0. La propiedad puede formularse para un punto a cualquiera: si \displaystyle \lim_{x\to a}f(x) = 0 entonces e^{f(x)}-1 \sim f(x) cuando x \to a. Para probarlo hay que recordar la definición de equivalentes: que e^{f(x)}-1 \sim f(x) cuando x \to a quiere decir que \displaystyle \lim_{x\to a}\frac{e^{f(x)}-1}{f(x)} = 1. Usando que \displaystyle \lim_{x\to 0}\frac{e^{x}-1}{x} = 1 y escribiendo la definición de límite para todos los límites involucrados se puede probar que esto es cierto (y es un buen ejercicio hacerlo).

Saludos