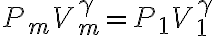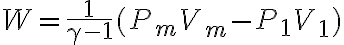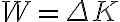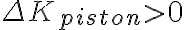Foro de Consultas Ejercicios y Teórico

Hola! Este ejercicio no me está dando y no se me ocurre otra forma de plantearlo. 

Usé la ecuación para un proceso adiabático para relacionar la presión y el volumen de la máxima compresión (Pm y Vm) con la presión y el volumen iniciales que me da la letra:

$P_mV_m^ \gamma = P_1V_1^ \gamma$   (1)

Después planteé la ecuación para el trabajo por dos caminos

$W= \frac{1}{ \gamma -1} (P_mV_m-P_1V_1)$    (2)

$W= \Delta K$  (3)

y pensé que para que la compresión sea máxima, W debe ser máximo, entonces \Delta K\ también. Impuse que la energía cinética final del móvil sea 0, reemplacé y resolví el sistema, pero no me da como la solución. Tengo dudas en las hipótesis de esta última parte, pero no se me ocurre de qué otra forma pensarlo. Agradezco desde ya su ayuda!!