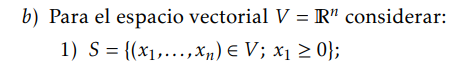Hola, en este ejercicio no sabría como escribir que S no es subespacio vectorial porque si tomo un K perteneciente a Rn menor que 0 daría que X1 no cumpliría la condición de ser mayor o igual a 0
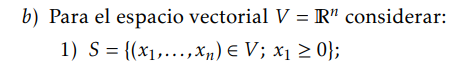
Hola, en este ejercicio no sabría como escribir que S no es subespacio vectorial porque si tomo un K perteneciente a Rn menor que 0 daría que X1 no cumpliría la condición de ser mayor o igual a 0