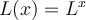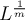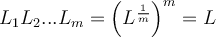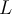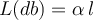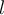Práctico 6 Ej. 1

Práctico 6 Ej. 1

de Guillermo Cossio Coppes -
Número de respuestas: 1

Buenas,

No me queda del todo claro por qué la solución considera que la atenuación 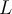L del canal es simplemente el largo por la atenuación por unidad de distancia.

Por como lo pensé yo, con los 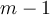m - 1 repetidores equiespaciados,  cada sección de canal tendría una atenuación 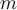m veces menor a la atenuación del canal entero, que al tomarse en su conjunto debería atenuar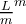 \frac{L}{m}^{m}

La solución me parece razonable si los repetidores estuvieran todos en el receptor o en el transmisor, pero no entiendo por qué el separar el canal en varias partes no cambia su atenuación total.

Desde ya muchas gracias!


Edit: Acabo de darme cuenta de que si separo el cable en 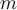m porciones, cada una de ellas debería tener atenuación 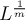L^{\frac{1}{m}} para que el canal tenga atenuación total 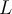L . Si eso está bien, no me queda claro cual es el sentido de dar una atenuación por kilómetro si al fin y al cabo la atenuación no escala linealmente con el largo.
En respuesta a Guillermo Cossio Coppes

Re: Práctico 6 Ej. 1

de Alejandra Armendariz -

Buenas, efectivamente es eso último que decís. Cuando trabajamos con medios duros, la atenuación la podemos modelar como L(x)=L^{x} donde x es la distancia normalizada entre 0 y 1.

Considerando que los repetidores se encuentran equiespaciados, tenemos que la atenuación de cada tramo de cable es idéntica para cada uno de ellos y vale L^{\frac{1}{m}}, por lo que la atenuación total en recepción resulta L_1L_2 ... L_m =\left ( L^{\frac{1}{m}} \right )^{m}=L.

Esta atenuación total (L) es un parámetro del cable y, en general, es una información que nos la brinda el fabricante. En este caso nos dan como dato la atenuación en db por kilómetro de cable, por lo que L(db)=\alpha \, l con l el largo total en kilómetros.

Saludos,

Alejandra.