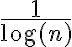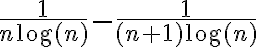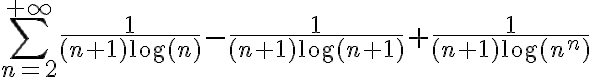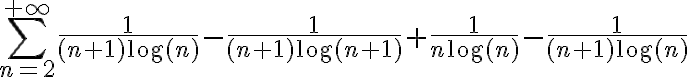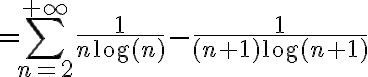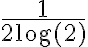Hola.
No sé como demostrar lo que me pide el ejercicio, intenté llegar a una telescópica a ver si se me cancelaban términos y me quedaba lo que esta a la derecha del igual, pero quedé trancado y veo cómo seguir.
Saludos
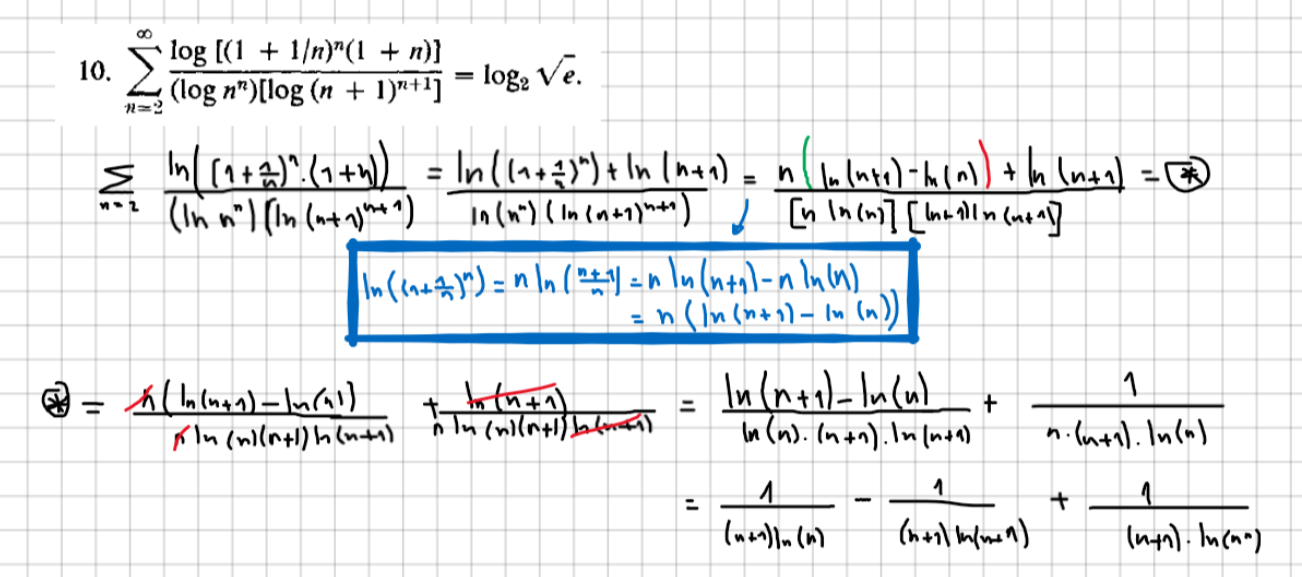
Hola.
No sé como demostrar lo que me pide el ejercicio, intenté llegar a una telescópica a ver si se me cancelaban términos y me quedaba lo que esta a la derecha del igual, pero quedé trancado y veo cómo seguir.
Saludos
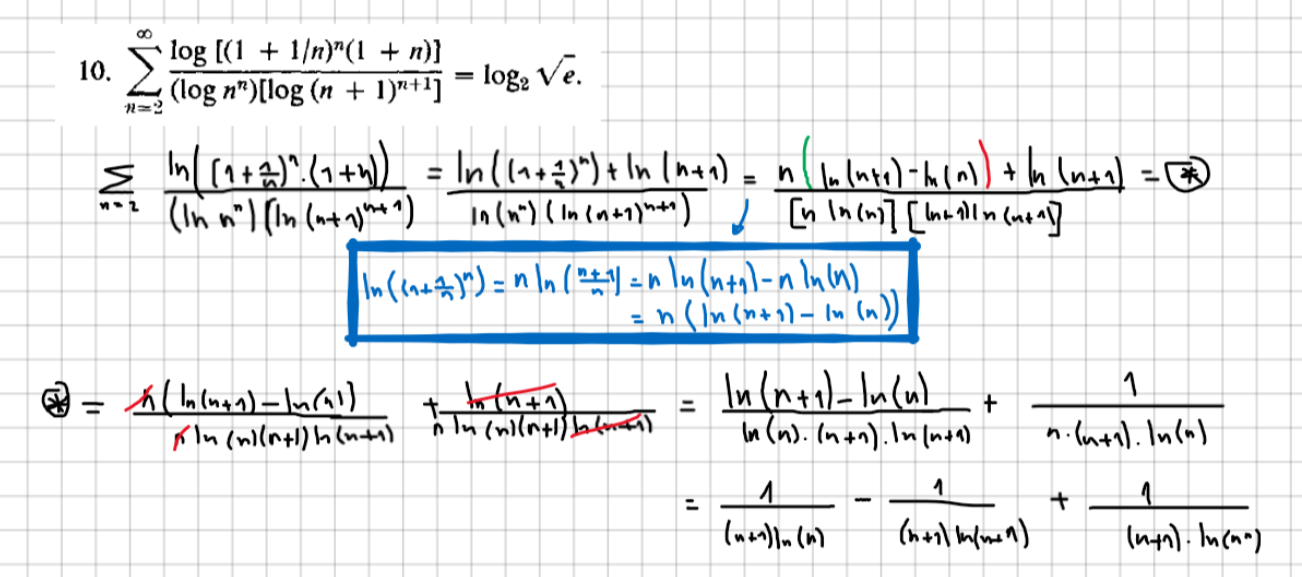
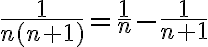
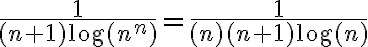 es la misma idea que la factorización anterior pero multiplicamos por
es la misma idea que la factorización anterior pero multiplicamos por