Foro de Ejercicios fuera de los Prácticos

Hola Joel. Fijate que esa ecuación de primer orden no es lineal  (no se puede escribir como algo de la forma 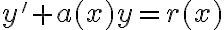$y'+a(x)y = r(x)$), por lo que no aplica lo de resolverla haciendo homogénea + particular. Ahí lo que podés hacer es pasar dividiendo el 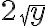$2\sqrt{y}$, lo que resulta en la ecuación

$\displaystyle \frac{y'}{2\sqrt{y}} -2\sqrt{y} = e^x$

Haciendo el cambio de variable 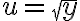$u = \sqrt{y}$, tenemos que 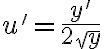$\displaystyle u'=\frac{y'}{2\sqrt{y}}$, por lo que podemos transformar la ecuación a 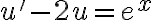$u'-2u= e^x$, que sí es una ecuación lineal y se resuelve haciendo homogénea + particular.

Saludos