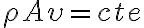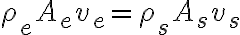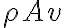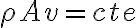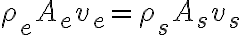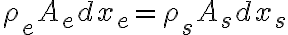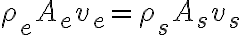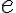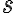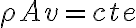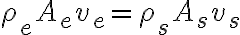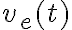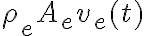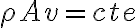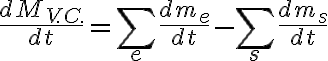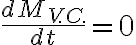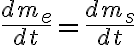F2 - 2S: Ecuación de continuidad

$\rho A\upsilon =cte$

¿Esto significa que la cantidad de masa de fluido que pasa por un punto (o área transversal) por unidad de tiempo es siempre constante? ¿Esto siempre es cierto aunque la velocidad con la que el fluido pasa por el punto no sea siempre constante?

Gracias

Re: Ecuación de continuidad

de Italo Bove - domingo, 19 de septiembre de 2021, 16:09

Las respuestas son Sí y No.

Toda ecuación de física SIEMPRE tiene un rango de validez, y jamás hay que extrapolarla más allá de dicho rango.

Por ende, tu pregunta tiene que transformarse a:

¿Cuáles son las condiciones necesarias para llegar a esa ecuación?

Esa ecuación es un caso particular de un caso particular de la ecuación de conservación de la masa o ecuación de continuidad.
En su forma general dice:
dM_vc/dt =sumatoria_i(dme_i/dt) - sumatoria_j(dms_j/dt)

M_vc: masa en un volumen de control
me_i: masa que entra por la entrada i
sumatoria_i: suma en todas las entradas
ms_j: masa que sale por la salida j
sumatoria_j: suma en todas las salidas

Como podrás ir viendo, desde la ec general a la que pusiste vos hay varios pasos que tienen que cumplirse
1) Una sola entrada y una sola salida
2) La masa en el volumen de control no cambia

Con esas dos condiciones todavía no llegamos a la ec que vos ponés sino a esta otra:

$\rho_e A_e v_e = \rho_s A_s v_s$

Dicha ecuación puede explicarse como: si tengo un volumen de control con una entra y una salida, y en el volumen la masa que tengo permanece constante en el tiempo, entonces lo que entra es igual a lo que sale.

Hasta acá no quiere decir que

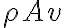
$\rho A v$ sea constante, puede variar en el tiempo (y por ende la masa que pasa por ese punto varía con el tiempo), pero con la condición que varíe igual en la entrada de tu sistema que en la salida.

Para imponer la condición

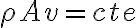
$\rho A v = cte$ falta una condición más:

2') El sistema es estacionario

Puse 2' pues si el sistema es estacionario, entonces la condición previa ( 2) M_vc = cte) ya se cumple.

Imponer que el sistema sea estacionario te obliga a que en cada punto de tu sistema las condiciones no cambian con el tiempo. Por ende v(x,t) = v(x), o sea, la velocidad en cada punto no cambia con el tiempo, y solamente puede cambiar si me muevo a otro punto.

Entonces ahí sí ahí se cumple tu ecuación. Pero como ves, tiene condiciones muy fuertes que se tienen que cumplir para llegar a ella.

Ahí sí la masa que pasa por ese punto es constante en el tiempo, pero necesito que la velocidad, la densidad y la sección de la cañería por donde pasa también lo sean.

Eso sí, tus variables pueden variar en el espacio, siempre que cumpla que el producto de las 3 sea constante independientemente del lugar del espacio donde mires.

Lamento lo largo de la respuesta, pero en física hay otra condición que se cumple siempre: cuanto más corta la pregunta, más larga la respuesta :)

Saludos

Italo

Re: Ecuación de continuidad

de Juan Agustín Rivero Szwaicer - martes, 21 de septiembre de 2021, 11:07

Ahhh. Quisiera repasar a ver si entendí bien. Decir que la masa que entra es igual a la que sale no sólo es decir

$\rho_e A_ev_e=\rho_sA_sv_s$ sino en realidad

$\rho_e A_edx_e=\rho_sA_sdx_s$ , y derivando eso respecto al tiempo llegamos a la igualdad anterior. Y decir que el volumen de control permanece constante no implica que el flujo sea estacionario, porque podrían haber otras cosas que puedan cambiar con el tiempo. ¿Es así?
Gracias

Re: Ecuación de continuidad

de Juan Agustín Rivero Szwaicer - martes, 21 de septiembre de 2021, 11:15

Ah, y otra cosa. Imponer que el flujo sea estacionario permite establecer

$\rho_eA_ev_e=\rho_sA_sv_s$ para todo punto

$e$ y

$s$ que nos tomemos entonces eso también implica que

$\rho Av=cte$ ?

Re: Ecuación de continuidad

de Nahuel Barrios - martes, 21 de septiembre de 2021, 20:09

Con las condiciones 1) y 2) de la respuesta de Italo se puede concluir que

$\rho_e A_e v_e=\rho_s A_s v_s$ .

Si el flujo no fuera estacionario podría ocurrir que la velocidad de entrada, por ejemplo, dependiera del tiempo:

$v_e(t)$ , lo que implicaría que

$\rho_e A_e v_e(t)$ también dependa del tiempo y por lo tanto no sea cte en el tiempo.

Para que

$\rho A v=cte$ necesitamos también, entonces, que las propiedades del fluido (concretamente la sección, velocidad y densidad) punto a punto no cambien con el tiempo, y esto es así para flujos estacionarios.

Nuevamente, te invito a repasar detenidamente la respuesta de Italo.

Saludos,

Nahuel

Re: Ecuación de continuidad

de Nahuel Barrios - martes, 21 de septiembre de 2021, 20:05

Hola Juan,

Italo parte de:

$\frac{dM_{V.C.}}{dt}=\sum_e \frac{dm_{e}}{dt}-\sum_s\frac{dm_{s}}{dt}$

que lo que quiere decir es que la variación de la masa del volumen de control en el tiempo se debe a las entradas o salidas de masa del volumen de control.

Si decimos que la masa que entra es igual a la que sale (la masa en el volumen de control permanece incambiada y por lo tanto

$\frac{dM_{V.C.}}{dt}=0$ ) y si tenemos una sola salida y una sola entrada se cumple:

$\frac{dm_e}{dt}=\frac{dm_s}{dt}$ y de allí podemos concluir que

$\rho_e A_e v_e=\rho_s A_s v_s$

Lo que acabo de explicar ya lo había mencionado Italo más detalladamente así que te invito a repasar detenidamente su respuesta.

Saludos,

Nahuel