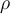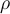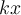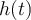Ejercicio 4.1.a

Ejercicio 4.1.a

de Agustina Behrens Lorenzi -
Número de respuestas: 8

Hola!! En el 4.1.a) me piden una expresión para la velocidad de entrada del agua a la bahía en función del tiempo. Tengo una duda de cuál es la velocidad que me piden calcular realmente. Por los datos de la gráfica y la ecuación de ondas sinuosidades llegué a:

vb(t)= -A.(2.pi/T). sen ((2.pi/T). t)

Ahora, me fije en las soluciones de este ejercicio el semestre pasado y veo que multiplica esta expresión por Ab/ Ac (área de la bahía sobre área del canal), lo cual no entiendo. Por ecuación de continuidad, eso debería hacer si estuviese calculando la velocidad en el canal, ya que:

Vc. Ac= Vb. Ab

Entonces, no entiendo por qué si me piden la variación de velocidad de entrada a la bahía se multiplica por Ab/Ac. ¿Es porque lo está tomando como que la velocidad de agua en el canal es la de entrada a la bahía? 

Gracias!!

En respuesta a Agustina Behrens Lorenzi

Re: Ejercicio 4.1.a

de Italo Bove -
Sí, efectivamente la velocidad de entrada a la bahía es la velocidad de agua en el canal.

La velocidad en la bahía (diferente a la velocidad de entrada a la bahía) sería solo una velocidad vertical sinusoidal en donde sube y baja una altura h0 en una frecuencia angular w=2pi/T (no está multiplicada por ninguna área).

Por cierto, la variación de altura máxima en la bahía es h0 = 1,5 m como se puede ver en la figura si se la mira con atención: la altura máxima es la 3ra raya, y en la 2da raya se dice 1,0 m. Trataremos de aclarar mejor eso en la letra del ejercicio.

Saludos,
Italo
En respuesta a Italo Bove

Re: Ejercicio 4.1.a

de Juan Agustín Rivero Szwaicer -
Hola. Cuando derivan la función del nivel del agua ¿no están calculando la velocidad del agua en subir y bajar? ¿Esta es proporcional a la velocidad con la que entra y sale el agua del canal?
No me queda muy claro, porque una velocidad sería en vertical y la otra en horizontal.
En respuesta a Juan Agustín Rivero Szwaicer

Re: Ejercicio 4.1.a

de Italo Bove -
El tema es que no se está relacionando velocidades, sino aplicando una ecuación, la de conservación de la masa.
La misma dice que el cambio en la masa de un volumen de control es igual a la masa que entra menos la que sale.
En este caso el volumen de control es la bahía. La densidad del agua se considera cte, y por ende
dM/dt = \rho dV/dt = \rho Area dh/dt

Acá hay una única entrada - salida. La variación de su masa es:
\rho A v,
con v la velocidad del agua en el canal.

Igualando las dos cosas te queda el vínculo entre las velocidades. Pero como dije, ello es consecuencia de la ecuación de conservación de la masa (o continuidad).

Saludos
Italo
En respuesta a Italo Bove

Re: Ejercicio 4.1.a

de Ariadna Belen Chiarlone Pereira -
Hola, profe. A mi me quedaron un par de dudas de este ejercicio. La primera es que con la ecuación de continuidad queda igualada la velocidad del canal con la de la bahía multiplicada por el factor Ab/Ac, pero la velocidad de la bahía es variable con el tiempo y la letra dice que la del canal es "uniforme con el tiempo"; no entiendo cómo pueden entonces vincularse entre sí. La otra es que, en el término sinusoidal originalmente yo incluí kx dentro del argumento de la función, pero no pude hallar k con los datos del problema. Al consultar las soluciones vi que no se incluyó, ¿Por qué es esto? Gracias!!
En respuesta a Ariadna Belen Chiarlone Pereira

Re: Ejercicio 4.1.a

de Nahuel Barrios -
Hola Ariadna,

cuidado, la letra dice que el agua "fluye con velocidad uniforme a lo largo de la sección entera del canal". Esto quiere decir que el valor de la velocidad del fluido es el mismo para todos los puntos de la sección del canal (o dicho de otro modo, que no depende la posición de los puntos en el canal). Que sea uniforme no significa que sea constante en el tiempo. De hecho la velocidad cambia en el tiempo, uniformemente. Por otra parte el término kx no tiene sentido en este contexto. No estamos hablando de una onda viajera sino de la dependencia de la altura con el tiempo, por lo tanto, se trata de una función h(t).
Saludos,
Nahuel