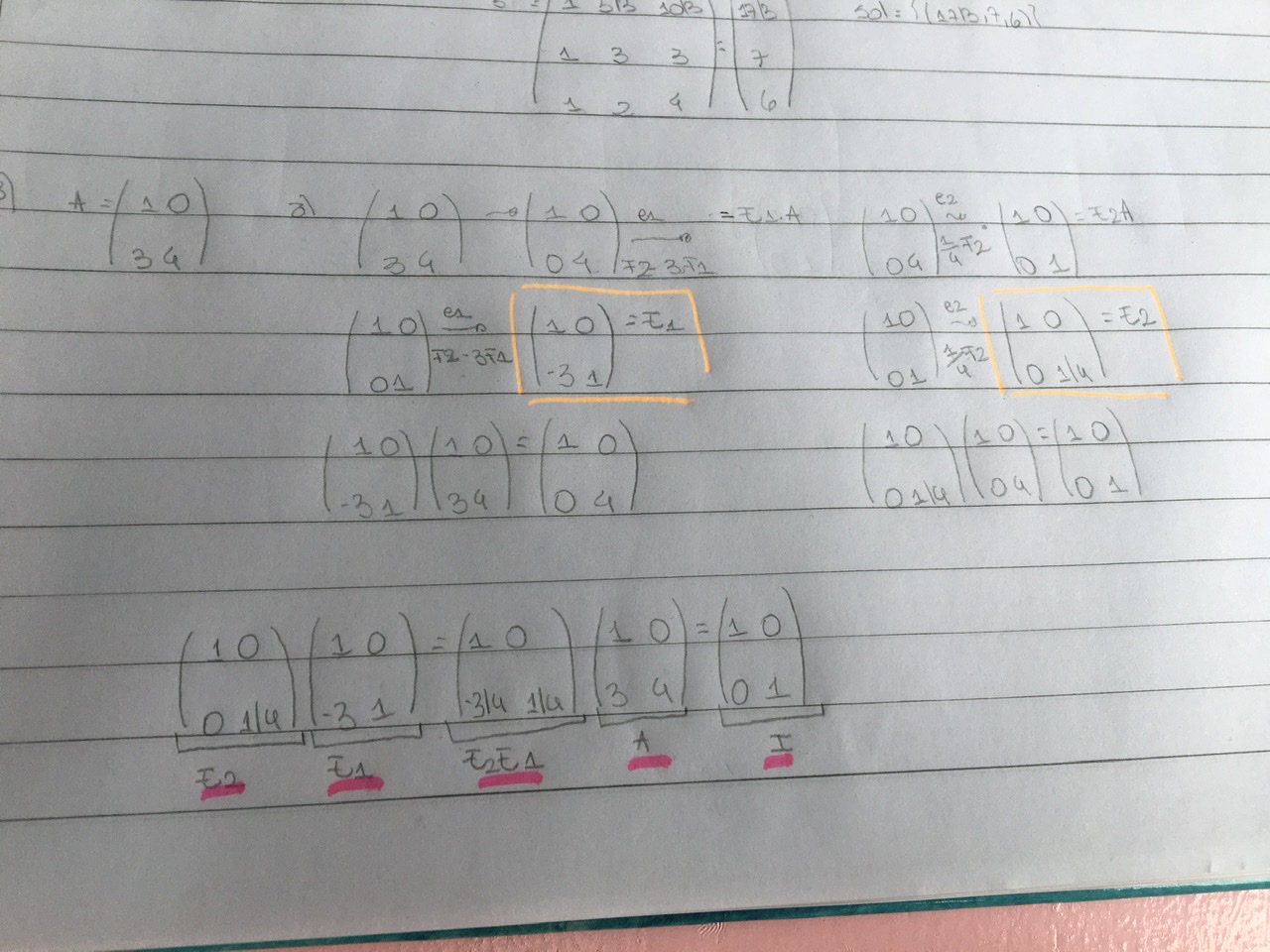Buenas noches me podrían dar una guía sobre este ejercicio?
Gracias!
Hola Camila,
Para ese ejercicio nos apoyamos en el teórico de las clases 8 y 9 donde se ve matrices elementales. La idea es que uses que a cada transformación elemental que yo le hago a una matriz (por ejemplo, restarle a la tercera fila 3 veces la primer fila) le puedo asociar una matriz elemental. Osea una matriz E que cumple que T(A)=EA (1) (Aplicarle transformacion T a la matriz A me da lo mismo que multplicar la matriz E por la matriz A, cualquiera sea la matriz A)
Para ese ejercicio nos apoyamos en el teórico de las clases 8 y 9 donde se ve matrices elementales. La idea es que uses que a cada transformación elemental que yo le hago a una matriz (por ejemplo, restarle a la tercera fila 3 veces la primer fila) le puedo asociar una matriz elemental. Osea una matriz E que cumple que T(A)=EA (1) (Aplicarle transformacion T a la matriz A me da lo mismo que multplicar la matriz E por la matriz A, cualquiera sea la matriz A)
Ahora podes probar de encontrar las transformaciones elementales que te llevan la matriz A a la matriz Identidad (son 2) y luego hallar las matrices asociadas a esas transformaciones.
Veamos que estas matrices son las que nos pide el ejercicio:
Si $$T_1$$ y $$T_2$$ son las transformaciones que encontramos y $$E_1$$ y $$E_2$$ son las respectivas matrices asociadas, tenemos por un lado que:
$$T_2 \circ T_1(A) =Id$$ (pues las elegimos para que tras aplicarselas a A nos de la identidad)
Y Por otro que usando (1) tenemos que:
$$T_2 \circ T_1(A) = T_2(T_1(A)) = T_2(E_1(A)) = E_2E_1(A)$$
$$T_2 \circ T_1(A) = T_2(T_1(A)) = T_2(E_1(A)) = E_2E_1(A)$$
es decir $$E_1$$ y $$E_2$$ cumplen que $$E_2E_1(A)=Id$$ como queriamos.
Se entiende?
cualquier cosa pregunta,
Saludos!
Adjunto el ejercicio porque no estoy segura de si es así la resolución.
Gracias!
Tu resolución es correcta si.
Saludos!
Saludos!
Muchas gracias!