Foro de Teórico

Hola Eugenia. Estás hablando de dos cosas diferentes. Por un lado, está la definición de convergencia de una serie: decimos que 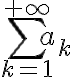$\displaystyle \sum_{k=1}^{+\infty} a_k$ converge si la sucesión de sumas parciales 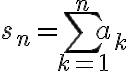$s_n = \displaystyle \sum_{k=1}^{n} a_k$ tiene límite. En caso que esa sucesión de sumas parciales (también llamada reducida n-ésima) tenga límite $L$, decimos que la serie converge a $L$. Ese $L$ puede ser cualquier real, no tiene por qué ser 0.

Por otro lado está la condición necesaria de convergencia, que habla sobre el término general de la serie. Lo que dice es que si la serie converge entonces 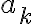$a_k$ tiene que tender a 0. Es decir, si la sucesión de sumas parciales 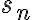$s_n$ tiene límite $L$, entonces la sucesión $a_n$ (el término general de la serie) tiene que tender a 0.

Espero que esto aclare tu duda. Saludos