Hola. La energía potencial me quedó en función de g y t^2. Para que me quede el resultado de las soluciones vy tendría que quedar igual a gt. No me doy cuanta por qué. Gracias por contestar
Estimada, en este ejercicio no actúa la aceleración gravitatoría y el resultado no depende del tiempo.
Lo que tenés que hacer es tomarte un diferencial de la energía potencial acumulada en un diferencial de cuerda e integrarlo espacialmente a lo largo de todo el pulso. Para eso, podés recurrir a la explicación de teórico sobre el origen del diferencial:
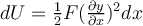
con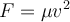
y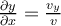
Saludos
Lo que tenés que hacer es tomarte un diferencial de la energía potencial acumulada en un diferencial de cuerda e integrarlo espacialmente a lo largo de todo el pulso. Para eso, podés recurrir a la explicación de teórico sobre el origen del diferencial:
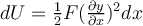
con
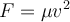
y
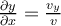
Saludos
Gracias. Pensé que era la energía potencial gravitatoria no la debido a F.
Pero si depende del tiempo tau que es el que demora la F en subir y también en bajar. Para la pregunta que te hice t es tau.
Supongo que lo que me querés decir es que la energía de la cuerda no depende del tiempo siempre y cuando no se disipe la energía.