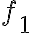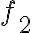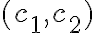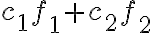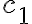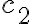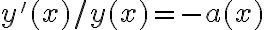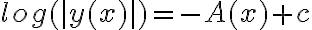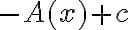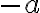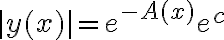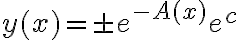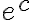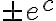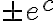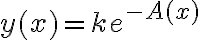Duda general sobre las constantes

Duda general sobre las constantes

de María Virginia Villar Gonzalez -
Número de respuestas: 4

Hola

No me quedó muy claro el tema de las constantes; sé que se agregan porque todos los múltiplos de la función solución son soluciones, ¿pero importa el lugar donde las pongo? ¿estaría bien sólo multiplicar la última expresión que obtenga por C y ya está? O en qué parte de la resolución tengo que empezar a operar con las constantes ya?

Aclaro que estoy hablando en el caso que no nos dan datos para que cumpla la función solución porque ahí sí que C es una función en particular.

Gracias

En respuesta a María Virginia Villar Gonzalez

Re: Duda general sobre las constantes

de Favio Piran -
Hola

¿A qué constantes te referís? No entendí bien la pregunta pero intento responder.
Si te referís a las constantes de la ec. lineal homogénea de orden 2 a coef constantes, en última instancia aparecen porque el espacio de soluciones de estas ecuaciones son un espacio vectorial (de dimensión 2).

Estas constantes son importantes porque funcionan como "coordenadas" dentro del espacio de soluciones. Es decir, si tenemos dos soluciones f_1 y f_2 que son linealmente independientes dentro del espacio de soluciones (es decir, una no es múltiplo de la otra), cada solución dentro del espacio de soluciones queda determinada por dos constantes (c_1, c_2) que corresponden a la función solución c_1f_1 + c_2f_2.

En definitiva, para encontrar una expresión para la ecuación general, alcanza con encontrar dos soluciones linealmente independientes. Luego, sus combinaciones lineales conforman el espacio de soluciones. Cada par de constantes corresponde a una solución distinta, y, como bien decís, si nos dan datos como f(0) y f'(0) podemos localizar una única de estas funciones dentro del espacio de soluciones (hallando c_1 y c_2 específicos).

Si la pregunta va por otro lado escribí abajo y respondo
Saludos!
En respuesta a Favio Piran

Re: Duda general sobre las constantes

de María Virginia Villar Gonzalez -
Hola, muchas gracias por la respuesta!
De todas formas, no era a esas constantes a las que me refería.
Las que me confunden son las que están como "k" en las soluciones. Según tengo entendido, salen de cuando en una ec. homogénea de 1er grado integrás los dos lados de la ecuación para despejar y(x). Como en las integrales de siempre, yo solo se las sumo al final de la resolución de la integral. Luego despejo la solución y(x) dependiendo del caso, normal. Pero me confunde porque en salgunos casos k termina multiplicando o restando y no entiendo cómo se llega a eso
Espero haberme explicado bien
Saludos!!
En respuesta a María Virginia Villar Gonzalez

Re: Duda general sobre las constantes

de Favio Piran -
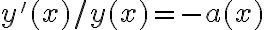
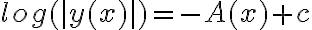
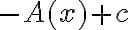
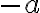
En la ecuación lineal homogénea de primer orden tenemos, despejando, y'(x)/y(x)=-a(x). Integrando en ambos lados y con un cambio de variable obtenemos que log(|y(x)|)=-A(x) + c donde -A(x) +c son todas las primitivas de -a (variando c tenemos todas las primitivas).
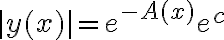
Ahora bien, despejando tenemos |y(x)|=e^{-A(x)}e^{c} y
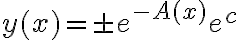
y(x)=\pm e^{-A(x)}e^{c}. Acá tenemos expresadas todas las posibles soluciones (salvo la constante y(x)=0).

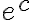
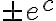
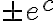
¿Dónde aparece la k? Como c es una constante arbitraria, e^c es una constante estrictamente positiva arbitraria. Luego \pm e^c es una constante no nula arbitraria. En lugar de poner \pm e^{c} como constante no nula arbitraria, escribimos k como constante no nula arbitraria. Ya sea moviendo k o moviendo c obtenemos todas las soluciones.
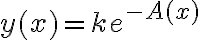
Con esta escritura tenemos que las soluciones se escriben como y(x)=ke^{-A(x)} donde k constante real arbitraria no nula. Como último detalle, si le permitimos a k ser nula, conseguimos la solución constante igual a 0, es decir, moviendo k en todos los reales obtenemos todas las soluciones.

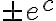
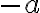
En definitiva, la constante k es un parámetro que hace referencia a los posibles valores \pm e^c donde c viene de las posibles elecciones de primitivas de -a.