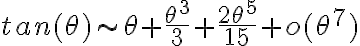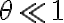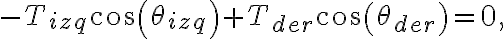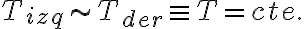Hola, una pregunta. ¿Por qué la ecuación de la onda en una cuerda no valdría también para ángulos grandes? Gracias
En respuesta a Juan Agustín Rivero Szwaicer
Re: Clase 1 Teórico-Práctico
¿Tendríamos que ser capaces de deducir la ecuación de la onda en una cuerda por nosotros mismos? Porque viendo el video me doy cuenta que hay tener en cuenta varios trucos como lo de la aproximación por ángulos chicos y poder escribir la tangente como ∂y/∂x, en vez de Δy/Δx y además poder evaluar esto en diferentes puntos.
Hola, interesantes preguntas.
No vale para ángulos grandes en parte por tu 2da pregunta, si no se puede aprox el seno del ángulo (que es la proyección tangencial de la fuerza) por la tangente entonces no se llega a la ec de la onda.
Además, si tomás la cuerda como un resorte, la tensión en la cuerda es proporcional al largo de la misma. Si las perturbaciones no son pequeñas, con una perturbación grande el largo de la cuerda aumenta, y entonces la tensión no es constante, aumentando con la perturbación. Es sin duda otro problema.
La tangente de un curva ES la derivada ∂y/∂x, y no Δy/Δx. Siempre. Solo cuando la curva es una recta ambas cosas son iguales. Ocurre que a uds. les enseñaron muchas veces a aproximar cantidades por la división de deltas, porque no sabían derivar.
En física (y en toda el conocimiento científico) los modelos tienen un rango de validez, que ustedes tienen que conocer: utilizar un modelo fuera de ese rango da error.
No creo que sean trucos, son herramientas matemáticas que ustedes conocen. Es cierto que hay que aprender a usarlas, pero con la práctica te sale naturalmente :)
Saludos
it
No vale para ángulos grandes en parte por tu 2da pregunta, si no se puede aprox el seno del ángulo (que es la proyección tangencial de la fuerza) por la tangente entonces no se llega a la ec de la onda.
Además, si tomás la cuerda como un resorte, la tensión en la cuerda es proporcional al largo de la misma. Si las perturbaciones no son pequeñas, con una perturbación grande el largo de la cuerda aumenta, y entonces la tensión no es constante, aumentando con la perturbación. Es sin duda otro problema.
La tangente de un curva ES la derivada ∂y/∂x, y no Δy/Δx. Siempre. Solo cuando la curva es una recta ambas cosas son iguales. Ocurre que a uds. les enseñaron muchas veces a aproximar cantidades por la división de deltas, porque no sabían derivar.
En física (y en toda el conocimiento científico) los modelos tienen un rango de validez, que ustedes tienen que conocer: utilizar un modelo fuera de ese rango da error.
No creo que sean trucos, son herramientas matemáticas que ustedes conocen. Es cierto que hay que aprender a usarlas, pero con la práctica te sale naturalmente :)
Saludos
it
Ahh, no sabía que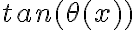 
era igual a 
. Tiene sentido.
Lo que entendí del todo es por qué las perturbaciones deben ser pequeñas, ni tampoco porqué esto implica tensión constante, ¿esto último es porque si hay una perturbación grande la cuerda hace fuerza para volver a su posición original, y eso hace que afecte la tensión?
Buenas, qué tal?
No sé si te respondieron fuera del foro pero va un intento de explicación...
que lo usás en la componente vertical de la segunda ley de Newton. Esto es porque si mirás el desarrollo de Taylor de estas funciones, su comportamiento es el mismo a ángulos pequeños:
No sé si te respondieron fuera del foro pero va un intento de explicación...
Pequeñas Oscilaciones:
Las perturbaciones deben ser pequeñas por eso que te comentaba Italo, en el régimen de pequeñas oscilaciones/ángulos pequeños podemos aproximar que lo usás en la componente vertical de la segunda ley de Newton. Esto es porque si mirás el desarrollo de Taylor de estas funciones, su comportamiento es el mismo a ángulos pequeños:
De esta forma, si 
despreciando todo lo que no es de orden dominante te queda:
despreciando todo lo que no es de orden dominante te queda:
Tensión Constante:
Esto a su vez implica que la tensión sea constante ya que considerando la segunda ley de Newton en su componente horizontal (
) tendrías que dado que el movimiento es transversal, las componentes horizontales de las tensiones a un lado y otro de un pequeño elemento de cuerda se deben anular. Es decir,
) tendrías que dado que el movimiento es transversal, las componentes horizontales de las tensiones a un lado y otro de un pequeño elemento de cuerda se deben anular. Es decir, 
siendo 
(
) el módulo de la tensión a la izquierda (derecha) del elemento de cuerda y análogamente los ángulos. Pero si usás los Taylor en torno a 0 (Maclaurin) es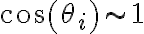 
y entonces concluís que:
() el módulo de la tensión a la izquierda (derecha) del elemento de cuerda y análogamente los ángulos. Pero si usás los Taylor en torno a 0 (Maclaurin) es 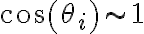y entonces concluís que:
Espero aclare,
Saludos