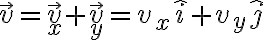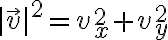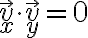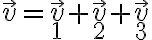Hola, Matías. Tu pregunta brinda una buena oportunidad para aclarar el cálculo.
La propiedad de que sobreviven los términos de igual versor es una consecuencia de que estos vectores son perpendiculares entre sí, y por eso su producto escalar es nulo.
El resultado general surge de aplicar que el producto escalar respeta la propiedad distributiva. Si tenemos un vector arbitrario escrito como la suma de otros dos,
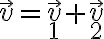 ,
,
su módulo (al cuadrado) se puede obtener desarrollando el producto escalar (prop. distributiva):

La propiedad de que sobreviven los términos de igual versor es una consecuencia de que estos vectores son perpendiculares entre sí, y por eso su producto escalar es nulo.
El resultado general surge de aplicar que el producto escalar respeta la propiedad distributiva. Si tenemos un vector arbitrario escrito como la suma de otros dos,
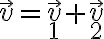 ,
,su módulo (al cuadrado) se puede obtener desarrollando el producto escalar (prop. distributiva):

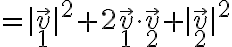
En definitiva, el razonamiento es el mismo que para el producto del binomio, pero con producto escalar.
Recuerda que, finalmente,
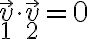 solo cuando alguno de los vectores es nulo o cuando son perpendiculares. El caso habitual sucede cuando se plantea un vector a partir de sus componentes de en una base ortonormal. Por ejemplo, en coordenadas cartesianas en el plano, un vector cualquiera se escribe como
solo cuando alguno de los vectores es nulo o cuando son perpendiculares. El caso habitual sucede cuando se plantea un vector a partir de sus componentes de en una base ortonormal. Por ejemplo, en coordenadas cartesianas en el plano, un vector cualquiera se escribe comoy su módulo (al cuadrado) se calcula a través de