Hola, Iván. No sé si estoy acertado, porque habría que revisar tu planteo, pero creo que tuviste suerte con la aplicación de las cardinales con algunos términos que casualmente se anulan.
- La primera cardinal se aplica para hallar la aceleración del centro de masas del cuerpo:
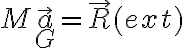
El movimiento del punto P no afecta esa relación, excepto en que la fuerza de fricción sea estática o dinámica.
- El sistema en estas condiciones tiene dos grados de libertad: uno para ubicar el punto G y otro para indicar la rotación del disco alrededor de su eje. Cuando no hay deslizamiento, el movimiento del centro G queda vinculado al ángulo de rotación. Este vínculo deja de cumplirse cuando hay deslizamiento.
- Para resolver el ejercicio hay que obtener dos ecuaciones (una para cada grado de libertad), combinando las cardinales, por ejemplo.
- Al aplicar la segunda cardinal hay que tomar en cuenta el movimiento del punto de aplicación. En el caso del punto P el planteo cambia según si consideras el punto P fijo en el espacio o el punto P perteneciente al cuerpo. En el primer caso algunos términos quedan más simples porque la velocidad y aceleración de P son directamente cero. En el segundo caso los términos que quedan más simples son otros, gracias a que la posición de P con respecto a G es fija.... En contraste, la segunda cardinal queda bastante sencilla en comparación al plantearla respecto a G.
Espero que estos comentarios ayuden a la comprensión del ejercicio.
Suerte,
NC
- La primera cardinal se aplica para hallar la aceleración del centro de masas del cuerpo:
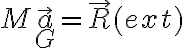
El movimiento del punto P no afecta esa relación, excepto en que la fuerza de fricción sea estática o dinámica.
- El sistema en estas condiciones tiene dos grados de libertad: uno para ubicar el punto G y otro para indicar la rotación del disco alrededor de su eje. Cuando no hay deslizamiento, el movimiento del centro G queda vinculado al ángulo de rotación. Este vínculo deja de cumplirse cuando hay deslizamiento.
- Para resolver el ejercicio hay que obtener dos ecuaciones (una para cada grado de libertad), combinando las cardinales, por ejemplo.
- Al aplicar la segunda cardinal hay que tomar en cuenta el movimiento del punto de aplicación. En el caso del punto P el planteo cambia según si consideras el punto P fijo en el espacio o el punto P perteneciente al cuerpo. En el primer caso algunos términos quedan más simples porque la velocidad y aceleración de P son directamente cero. En el segundo caso los términos que quedan más simples son otros, gracias a que la posición de P con respecto a G es fija.... En contraste, la segunda cardinal queda bastante sencilla en comparación al plantearla respecto a G.
Espero que estos comentarios ayuden a la comprensión del ejercicio.
Suerte,
NC
