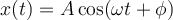Hola, buenas! Tenía una duda sobre el ejercicio 6. Logré calcular Vo y Wo, pero no logro sacar Xo. Se me ocurrió una forma de resolverlo igualando la fuerza elástica con la peso antes de que la bala impactara contra la masa M, pero en el resultado final me estaría quedando M grande en vez de m chica como se muestra en las soluciones. Si me podrían pasar un pique para resolverlo... Desde ya, muchas gracias!
Hola, Valentina
Para hallar la amplitud del movimiento debes primero escribir la solución general para la posición en función del tiempo. Recuerda que si llegaste a una ecuación de movimiento de la forma:
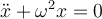
Para hallar la amplitud del movimiento debes primero escribir la solución general para la posición en función del tiempo. Recuerda que si llegaste a una ecuación de movimiento de la forma:
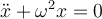
Entonces la solución general debe ser de la forma:
Donde A es la amplitud del movimiento oscilatorio y ϕ la constante de fase. Esos dos parámetros pueden determinarse imponiendo las condiciones iniciales, es decir, la posición y la velocidad en tiempo t = 0. ¿Te das cuenta cómo seguir a partir de acá?
Fijate si podés encararlo por ahí y cualquier cosa volvé a preguntar.
¡Saludos!
Carla, muchas gracias por tu respuesta! Intentaré fijarme si logro encararlo con esto que me decís.
Hola, que tal?
No estoy sabiendo como terminar este ejercicio. Llegué a la solución del movimiento armónico vertical visto en el teórico:
y(t)=A*cos*(wt + phi) + ye donde ye es la posicion de equilibrio: ye=lo + (m/k)* g
Calculé la velocidad despues de impacto utilizando el impetu lineal: v=(m*v)/(m+M)
Pero no se como continuar. Si uso las condiciones iniciales y asumo lo=0, el resultado me da diferente.
Me pueden dar una ayuda?
Gracias
No estoy sabiendo como terminar este ejercicio. Llegué a la solución del movimiento armónico vertical visto en el teórico:
y(t)=A*cos*(wt + phi) + ye donde ye es la posicion de equilibrio: ye=lo + (m/k)* g
Calculé la velocidad despues de impacto utilizando el impetu lineal: v=(m*v)/(m+M)
Pero no se como continuar. Si uso las condiciones iniciales y asumo lo=0, el resultado me da diferente.
Me pueden dar una ayuda?
Gracias
Hola Diego.
El problema es que estás usando una solución para una sola masa. El movimiento oscilatorio es para ambas masas unidas.
El calculo que hacés para la velocidad es correcto.
Para continuar, intentá tomar la solución y(t) e imponer las condiciones iniciales. Fijate que la condición y(0) viene dada por el equilibrio del bloque M, y la condición v(0) por la velocidad que calculaste.
Saludos!
El problema es que estás usando una solución para una sola masa. El movimiento oscilatorio es para ambas masas unidas.
El calculo que hacés para la velocidad es correcto.
Para continuar, intentá tomar la solución y(t) e imponer las condiciones iniciales. Fijate que la condición y(0) viene dada por el equilibrio del bloque M, y la condición v(0) por la velocidad que calculaste.
Saludos!
Lo escribí mal en el mensaje anterior, estoy usando las dos masas. Intenté realizar de nuevo el ejercicio y sigo obteniendo un resultado diferente. Me queda lo siguiente:
y(t)=A*cos*(wt + phi) + ye con ye=(m+M)*(g/k)
y'(t)=A*w*sen(wt + phi)
y(0)=ye donde obtengo que phi=pi/2
y'(0)=(m*v)/(m+M) donde obtengo A=m*v/(raiz((m+M)/k))
Mirando el resultado, entiendo que mi problema está relacionado al punto de equilibrio, ya que en la solucion aparece g. No se si realizan los cálculos utilizando las ecuaciones del armónico horizontal y luego "trasladan" el punto para que tenga el cuenta el punto de equilibrio. No se me ocurre mas nada ya
y(t)=A*cos*(wt + phi) + ye con ye=(m+M)*(g/k)
y'(t)=A*w*sen(wt + phi)
y(0)=ye donde obtengo que phi=pi/2
y'(0)=(m*v)/(m+M) donde obtengo A=m*v/(raiz((m+M)/k))
Mirando el resultado, entiendo que mi problema está relacionado al punto de equilibrio, ya que en la solucion aparece g. No se si realizan los cálculos utilizando las ecuaciones del armónico horizontal y luego "trasladan" el punto para que tenga el cuenta el punto de equilibrio. No se me ocurre mas nada ya
Ok. Supongo que a ese 'ye' ahora le falta el término 'lo', ¿verdad?.
Cuando decís "y(0)=ye donde obtengo que phi=pi/2" no es del todo correcto.
y(0) es la posición de equilibrio para el bloque M (la posición inicial en el MAS), y también es igual a A*cos*(phi) + (m+M)*(g/k) +lo (que viene de sustituir t=0 en y(t)).
¿Se entiende?
Cuando decís "y(0)=ye donde obtengo que phi=pi/2" no es del todo correcto.
y(0) es la posición de equilibrio para el bloque M (la posición inicial en el MAS), y también es igual a A*cos*(phi) + (m+M)*(g/k) +lo (que viene de sustituir t=0 en y(t)).
¿Se entiende?
Muchas gracias!!