Foro Práctico VIII

Hola, Seylen. Me alegra ver que no le tienes miedo a las cuentas!! :-)

Está algo difícil de revisar el planteo, pero parece ser que en realidad tu momento angular para la barra es correcto y coincide con el de la solución publicada.

La solución está escrita usando vectores de distintas bases, la de ejes principales y un término según el versor 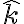$\hat k$.

Se puede desarrollar este término usando la descomposición del versor que tienes planteada: 

$4mL^2 \dot \varphi \hat k = -4mL^2 \dot \varphi \cos\theta \hat e_r + 4mL^2 \dot \varphi \sin \theta \hat e_\theta$

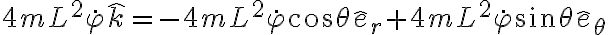
y luego de agrupar los resultados con los demás términos, llega a la misma expresión que obtuviste. Como más adelante se hace la proyección con 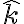$\hat k$, no hay una ventaja para el cálculo en reescribir el momento angular de esta manera.

Me parece excelente que hayas hecho un planteo alternativo usando los elementos que hemos aprendido en el curso. Eso es genial para poder verificar y comprobar si estamos entendiendo los temas. La contra que le veo es que luego de trasladar el tensor de inercia, no quedas en una base de ejes principales y eso conduce a la aparición de elementos fuera de la diagonal. Como estamos haciendo las cuentas a mano, esto implica un tiempo de cálculo sustancialmente mayor; llegado el momento del parcial o examen es preferible ir por el camino más corto.

Saludos,
NC