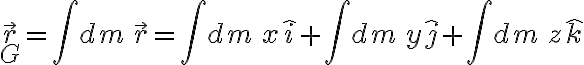Foro de consultas generales

Hola, Iván. Se ve que quisiste hacer un cálculo simple, pero desafortunadamente está mal planteado.

Observa que si aplicas tu método para un círculo completo llegarías a que el centro de masa aparece en 4R/3 separado de su centro geométrico. No sé a vos, pero no me convence...

Ya desde el comienzo del planteo hay un error grave, al igualar un vector a un escalar (la posición del centro de masa y la integral que planteaste). En cambio, se podría poner

$\displaystyle \vec r_G = \int {dm \, \vec r} = \int{dm \, x} \hat i + \int{dm \, y} \hat j +\int{dm \, z} \hat k$

usando como ejemplo coordenadas cartesianas. Luego es posible usar argumentos de simetría para concluir cuáles de los términos son nulos o no.

¿Cómo podrías elegir la orientación de los ejes x, y, z para poder usar el razonamiento de que el centro de masas está sobre la línea que divide al semicírculo en dos partes iguales?

Una observación final: es más sensato plantear esta descomposición de la integral en coordenadas cartesianas primero y después resolver las integrales faltantes en coordenadas cilíndricas, en lugar de tratar de escribir el vector de posición 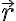$\vec r$ directamente en coordenadas cilíndricas. ¿Te das cuenta de cuál sería diferencia?

Saludos,

NC