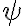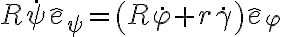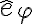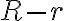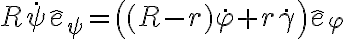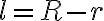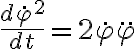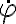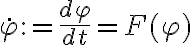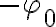MecNew: Segundo parcial 2011

Buenas, me surgieron un par de dudas al realizar el primer ejercicio.

En primer lugar no comprendo por que psi y phi son diferentes. Yo razoné que si rueda sin deslizar, entonces el punto de contacto que esta en el tubo debe girar siempre alineado con el centro de masa del cilindro. De todos modos no llegue a esto con mis cálculos, entonces vi la solución y el planteo es diferente al mío.

Lo que yo hice fue plantear distribución de velocidades entre el punto de contacto y el centro de masa (ambos del cilindro) e igualarlo a la velocidad de el punto de contacto en el tubo. Así obtuve:

R (psi punto) según epsi= [R (phi punto) + r (gamma punto)] según ephi

Siendo gamma el ángulo con el que gira el cilindro sobre su propio eje (pido disculpas por la notación).

No entiendo que estoy planteando mal ni por que psi y phi son diferentes.

Si me pudieran guiar sería de mucha ayuda.

Muchas gracias, saludos!

Re: Segundo parcial 2011

de Nicolás Casaballe - domingo, 4 de julio de 2021, 21:00

Hola, María Belén. Veamos si podemos aclarar estas dudas.

(*) Los ángulos $\psi$ y $\varphi$ son diferentes:

El ángulo 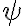$\psi$ indica la rotación del tubo alrededor de su eje. Esta coordenada no hace referencia al cilindro en el interior del tubo, así que por ahora vamos bien.

El ángulo $\varphi$ indica el ángulo que forma con la vertical la línea que va del centro del tubo y al centro del cilindro. Como el centro del tubo está fijo, este ángulo termina dependiendo solamente de la posición del cilindro.

En principio estas coordenadas son independientes (hay dos grados de libertad). Podría suceder que, debido a los vínculos del sistema, el movimiento terminase cumpliendo $\psi=\varphi$ . Sin embargo, la condición de rodar sin deslizar no corresponde a tal vínculo.

Una manera de convencerse de que los ángulos son diferentes es pensar en el caso sencillo en el cual el tubo se mantiene completamente inmóvil (mediante algún agente externo). Entonces nos queda $\psi = \text{cte.}$ , mientras que el cilindro puede recorrer libremente el interior del tubo y conseguir valores arbitrarios de $\varphi$ , incluso si rueda sin deslizar.

(*) Distribución de velocidades:

- Permíteme escribir la relación que pusiste en tu mensaje en latex (no te preocupes por escribirlo así; se entendió lo que pusiste):

$R \dot \psi \hat e_\psi = \left(R\dot \varphi + r \dot \gamma \right ) \hat e_\varphi \qquad {}$ (?!)

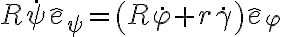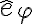Algo muy interesante que estás haciendo es utilizar versores $\hat e_\psi$ y $\hat e_\varphi$ por separado. Me parece que conceptualmente está perfecto, puesto que (como vimos antes) los ángulos son independientes. Pero para que la identidad vectorial sea posible, ambos versores deben coincidir. Demostrar que eso sucede es un "detallecito", pero hay que hacerlo.

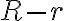- La expresión anterior tienen un error, debido a que la velocidad del centro del cilindro no está bien hallada. Recuerda que, en este sistema, la variable $R$ representa el radio interior del tubo y $r$ el radio del cilindro. Entonces, la distancia entre sus centros es $R-r$ en lugar de $R$ . Cuando hiciste la distribución de velocidades te quedó la distancia incorrecta. Una vez corregido esto, te debería quedar

$R \dot \psi \hat e_\psi = \left ((R-r) \dot \varphi + r \dot \gamma \right) \hat e_\varphi$

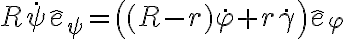
En la solución publicada se define la variable auxiliar 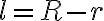$l = R -r$ y se escribe la ecuación anterior con ella.

(*) Determinación de la ecuación de movimiento

En la solución se resuelve la primera parte a partir de aplicar las ecuaciones cardinales a los cuerpos. ¿Pensaste alguna manera alternativa de obtener la ecuación de movimiento? Por ejemplo, ¿qué pasa si tomamos en cuenta alguna cantidad conservada en el sistema?

----

Estoy seguro de que a medida de que vayas resolviendo algunos ejemplos más, esto te va a resultar más natural. No dudes en consultar nuevamente si hace falta.

Suerte,
NC

Re: Segundo parcial 2011

de Julieta Merlo Dominguez - lunes, 5 de julio de 2021, 10:22

Hola! yo tengo una consulta sobre la parte b del ejercicio 1 de este mismo parcial. Dice que observando que el movimiento del cilindro es periódico debo encontrar una expresión integral para el período del movimiento, no se me ocurrió ninguna forma de resolverlo entonces acudí las respuestas. allí plantea la integral de φ´ producto con φ´´. No entiendo de donde sale esto, estaría necesitando alguna guía para esta parte del ejercicio.
Desde ya muchas gracias

Re: Segundo parcial 2011

de Nicolás Casaballe - lunes, 5 de julio de 2021, 13:28

Hola, Julieta. La letra puede resultar bastante críptica planteada de esa manera; yo tuve que detenerme a pensar un rato para entender a qué se refería, y afortunadamente había visto algunos problemas similares. Hay varias consideraciones para hacer antes de llegar a la respuesta.

- La ecuación de movimiento que se obtiene no se puede resolver analíticamente. No vamos a contar con una ley horaria $\varphi (t)$ .

- La ecuación de movimiento a la que se llega es análoga a la de un péndulo, sin la aproximación de oscilaciones de pequeña amplitud.

- Es posible hacer una preintegración de la ecuación de movimiento. Esto es gracias a que, en general, podemos plantear las derivadas

$\dfrac {d\dot \varphi ^2}{dt} = 2 \dot \varphi \ddot \varphi$

además de que para una función $f(\varphi)$ arbitraria se tiene (regla de la cadena):

$\dfrac {d f(\varphi)}{dt} = \dfrac {df(\varphi)}{d\varphi} \dfrac{d\varphi}{dt}=f'(\varphi) \dot \varphi$

Entonces, si multiplicamos cada término por $\dot \varphi$ , podemos integrar en el tiempo y usar las relaciones anteriores para hallar las primitivas. Observemos que para muchos casos, esto es prácticamente el cálculo de la energía del sistema.

- El resultado de estas operaciones permite pensar $\dot \varphi$ como función de la coordenada $\varphi$ en lugar de como función del tiempo:

$\dot \varphi := \dfrac {d\varphi}{dt}= F(\varphi)$

- ...eso nos permite (*) "despejar dt":

$dt = \dfrac{d\varphi}{F(\varphi)}$

(*) en realidad estamos planteando un cambio de variable a través de la derivada de la función inversa, pero muchos físicos tienen alergia a decirlo de esa manera -- y una notación más rigurosa termina resultando engorrosa.

- Planteamos la mitad del período como el tiempo que tarda el sistema en pasar de $-\varphi_0$ a $\varphi_0$ :

$\displaystyle \dfrac T 2 = \int_0^{T/2}{dt}=\int_{-\varphi_0}^{+\varphi_0} \dfrac{d\varphi}{F(\varphi)}$

y por último se multiplica el resultado por 2. Dejo para que mediten por qué no se puede calcular directamente el período y por qué elegimos calcular solo la mitad.

Espero que se haya comprendido. Una observación interesante es que estos pasos se pueden hacer también realizar para un oscilador armónico ideal y se puede obtener de forma analítica, no solamente el período, sino que también la ley horaria.

(otra observación no tan interesante, pero chistosa, es que en la solución le llaman T tanto al período y como a la componente tangencial de la reacción, y faltó poco para que T sea la energía cinética también).

Saludos,

Re: Segundo parcial 2011

de Ignacio Martin Acher Capozzoli - lunes, 5 de julio de 2021, 16:27

Hola, me surgió una duda al hacer la parte a del ejercicio 1. En las preguntas anteriores y en la solución veo que asumen que la velocidad angular del cilindro es gamma punto. ¿Por que es solo gamma punto y no phi punto mas gamma punto? De esta forma no estaríamos viendo el movimiento circular que hace el centro de masa sobre el tubo (con phi punto) y después el giro del cilindro sobre si mismo (con gamma punto)?
Desde ya muchas gracias

Re: Segundo parcial 2011

de Ricardo Marotti - lunes, 5 de julio de 2021, 17:35

Estimado:

La respuesta a esta pregunta depende de qué consideres es el ángulo gamma.

En la solución se indica un ángulo gamma en sentido antihorario. Para que su derivada sea la velocidad angular del cilindro, este ángulo tiene que ser el ángulo entre una recta solidaria al cilindro y una recta fija (por ejemplo la vertical).

Si midieras el ángulo gamma respecto a la recta que uno los dos centros de los cilindros (en el plano de la figura), entonces si la velocidad angular del cilindro debería ser gamma punto más phi punto.

El ejercicio se puede hacer simplemente llamándole omega a la velocidad angular del cilindro y no preocuparse de más nada.

Saludos:

Ricardo.