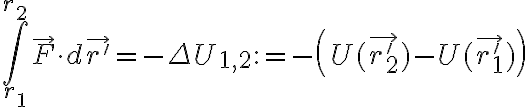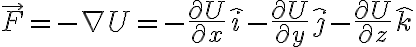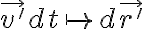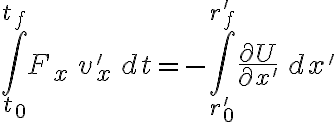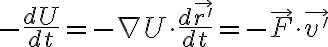Buenas. En la solución del ejercicio cuando integra la expresión de las fuerzas con las aceleraciones multiplicado por la velocidad relativa dice que las fuerzas conservativas por la velocidad relativa corresponde al trabajo en términos de su potencial, esa relación no me quedó muy claro cómo se deduce, cómo se llega a esa conclusión? Saludos.
Re: Ejercicio 2(a), segundo parcial 2019
Hola, Lucas. Lo que se usa en ese cálculo es consecuencia de la definición de una fuerza conservativa. El hecho de que aparezcan las velocidades y posiciones relativas no cambia el razonamiento.
Si cierta fuerza 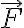 es conservativa, se sabe que existe cierto potencial escalar
es conservativa, se sabe que existe cierto potencial escalar 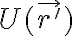 tal que el trabajo de la fuerza se puede determinar mediante las variaciones en esta función:
tal que el trabajo de la fuerza se puede determinar mediante las variaciones en esta función:
(el signo negativo en el potencial es por convención). La parte que preguntas es, en el fondo, la aplicación de esta definición para calcular el trabajo.
Matemáticamente, la relación anterior equivale a decir que la fuerza conservativa proviene del gradiente de la función escalar:
Recuerda que el gradiente es una generalización de la derivada, para funciones de varias variables. Esto es lo que se aparece en la solución, junto con un cambio en las variables de integración, para pasar de una integral en el tiempo a una integral de camino, usando
Miremos por ejemplo la componente x' de la fuerza por separado, para que quede más claro:
y relaciones análogas para las componentes y', z'. La suma de estas relaciones corresponde a la ecuación anterior, que puede ser vista como una generalización del teorema fundamental del cálculo.
-----
Otro camino equivalente es plantear la definición de la potencia de las fuerzas conservativas a partir de la derivada temporal del trabajo W:
Como 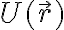 depende de la posición, hay que aplicar la regla de la cadena en el último término:
depende de la posición, hay que aplicar la regla de la cadena en el último término:
lo cual finalmente permite completar la demostración que queríamos, pero yendo en la otra dirección.
----
Esto parece complicado, porque lo es, pero espero que se haya podido aclarar un poco la situación. No dudes en consultar de nuevo si es necesario.
Saludos,
NC