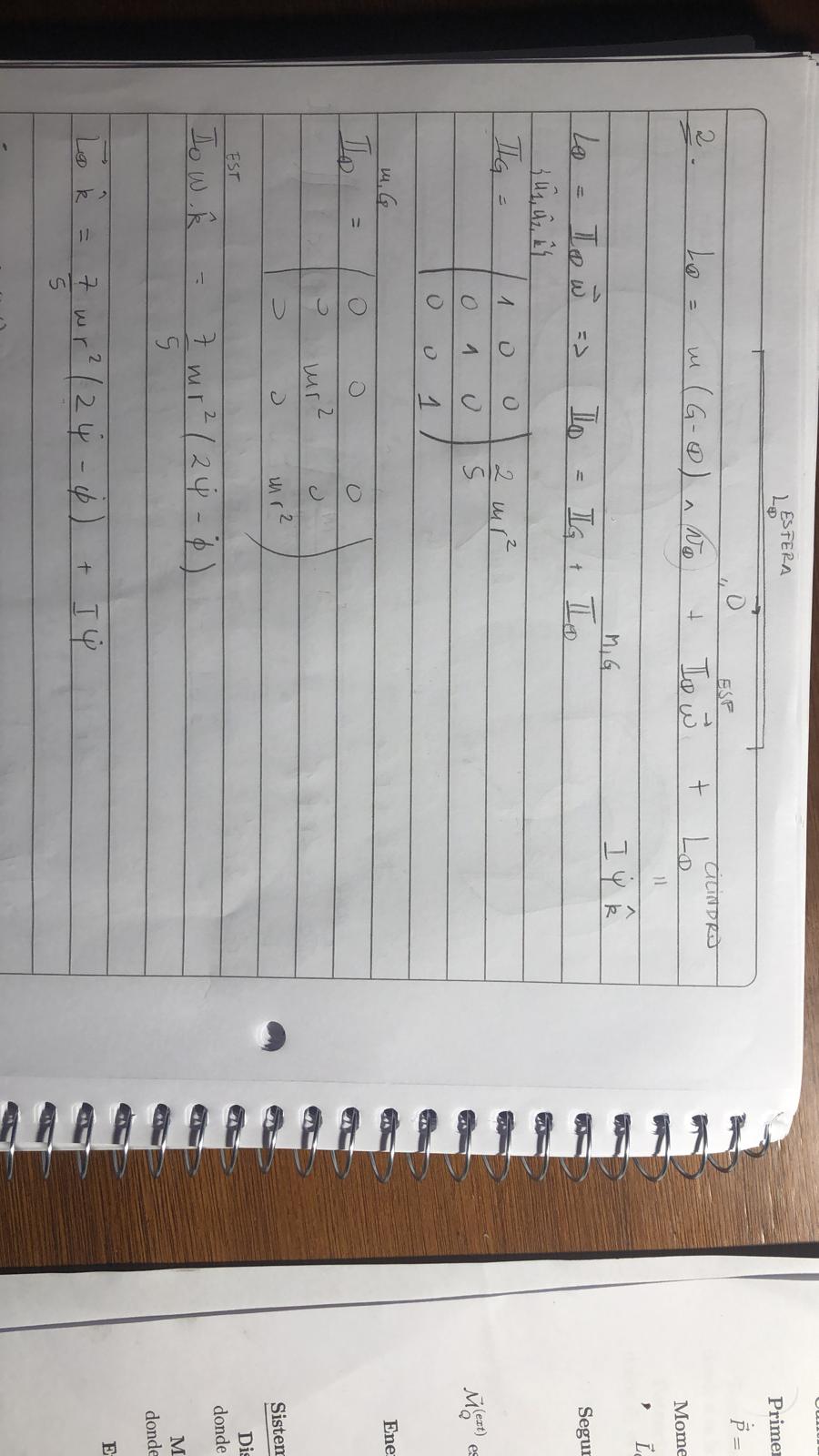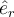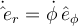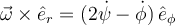Es una buena observación. Sucede que, gracias a la simetría esférica, el tensor de inercia con respecto al centro queda proporcional a la identidad. De esa manera, se obtiene que, para esa simetría, el momento angular respecto al centro queda siempre paralelo a la velocidad angular. Por eso surge la sutileza de que allí se puede usar un sistema de referencia orientado en forma arbitraria y *aparenta* ser un sistema solidario.
Esto se haría más evidente si, por ejemplo, el cuerpo no tuviese simetría esférica (una esfera no homogénea, digamos). En ese caso el tensor de inercia no sería proporcional a la identidad -- el momento angular y la velocidad angular no serían necesariamente paralelos. En una situación así, la solución es buscar los ejes principales para escribir el tensor de inercia y se escribir la velocidad angular en la base correspondiente.
En la solución publicada se esquiva un poco el problema aprovechando la simetría y haciendo los cálculos respecto a G (no se necesita, de hecho, plantear explícitamente todas las componentes del tensor de inercia).