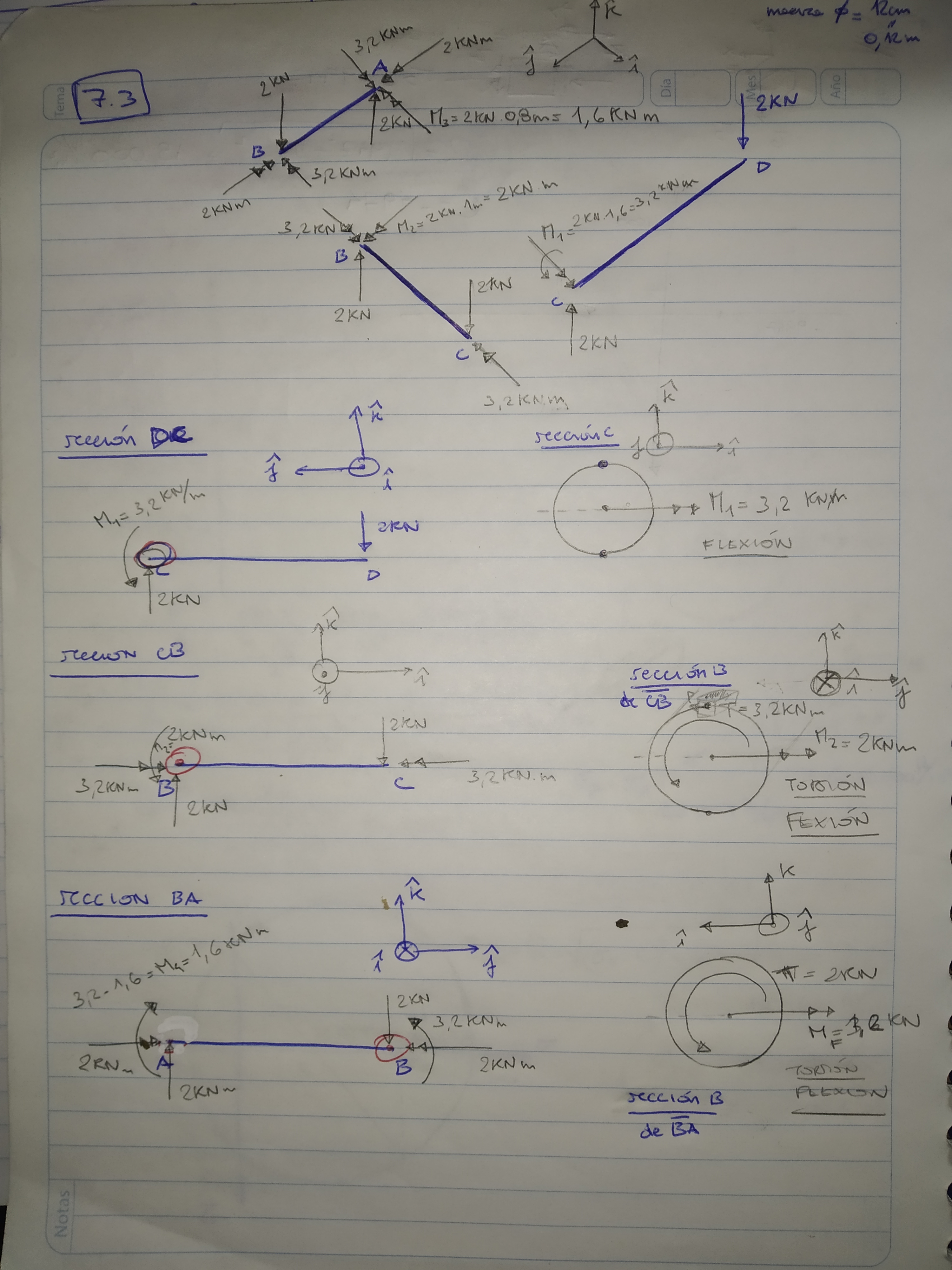
Estimado,
Los resultados a los que llegas están bien, lo que está mal es el círculo de Mohr aunque no se en donde exactamente.
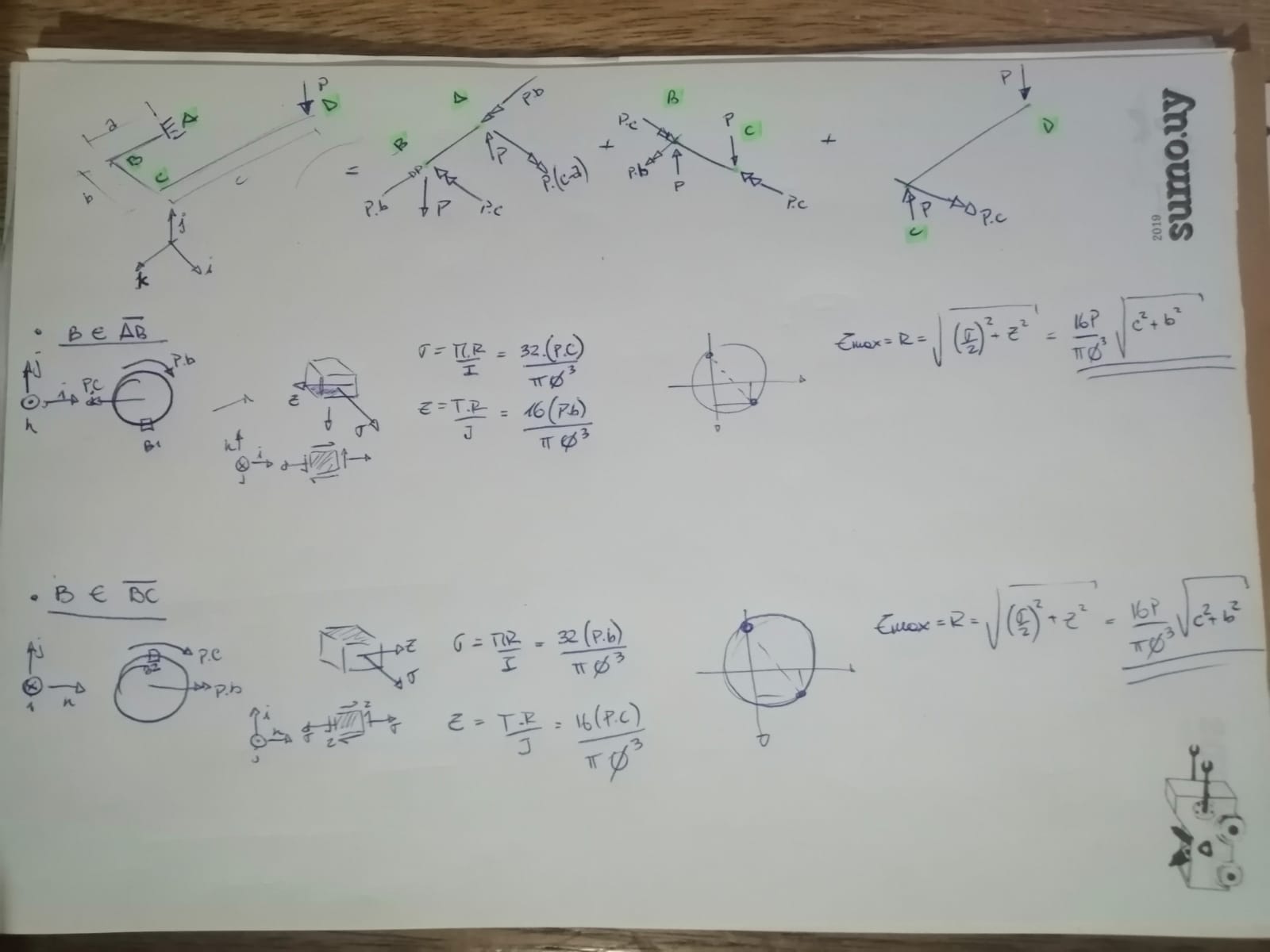
Antes de pasar a explicar más en profundidad debemos pensar un segundo en que es lo que estamos diciendo al decir: B de AB o B de BC.
La verdad es que lo que estamos diciendo es como lo estamos mirando, si perteneciendo a una barra o a la otra, si embargo, es el mismo punto!
De esta forma, físicamente debería estar igual de comprometido independientemente de desde donde se lo mire.
En la práctica, esto ocurre siempre y cuando no hagamos simplificaciones, por ejemplo, si en la barra BC tuvieramos además una carga axial, la carga se transfiere a la barra AB (a través de B) como una carga cortante, y como nosotros despreciamos los esfuerzos que la carga cortante genera sobre las piezas, ahí quedaría más comprometido B visto desde BC, porque no solo tendríamos flector y torsor (como en B perteneciente a AB) sino que también carga axial.
No obstante, para este caso, solo tenemos flectores que se transforman en torsores y viceversa, por lo tanto, si consideramos que el punto mas comprometido es aquel que tiene el esfuerzo cortante máximo, entonces es indiferente desde donde se mire.
Adjunto una foto donde demuestro esto último.