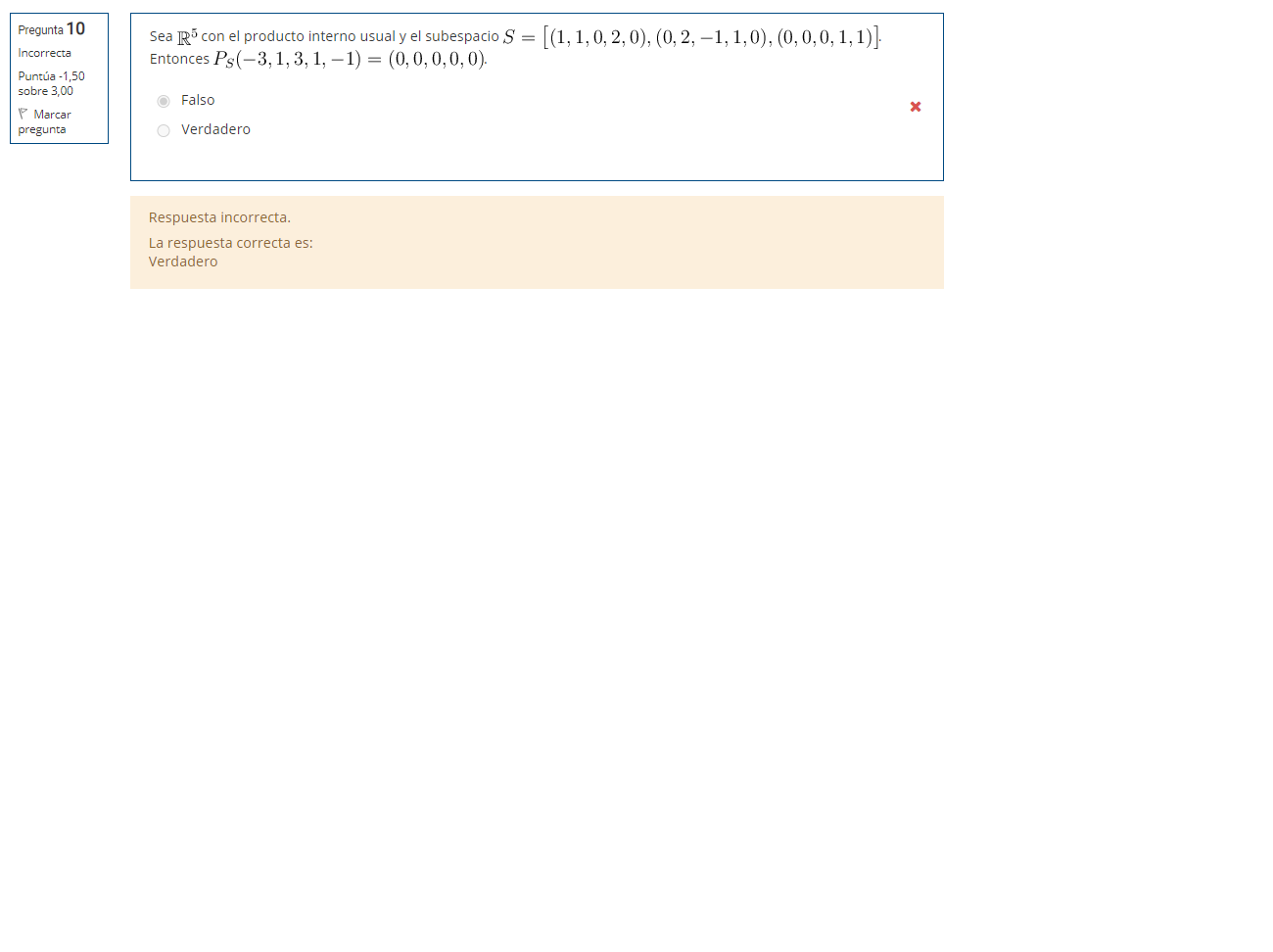
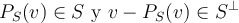Duda ej. de 2do parcial

Duda ej. de 2do parcial

de Valentin Albornoz Zipitria -
Número de respuestas: 6

Buenas Tendo una duda en el ejercicio que adjuntare luego de dar mi explicacion. A mi punto de vista tengo 2  justificaciones; -la primera es porque si vos hallas S⊥ , si tomas un vector cualquiera de S⊥ y le haces la proyeccion sobre S te va a dar 0 y el vector "v" (-3,1,3,1,-1) que pide hallar su proyeccion en S da 0 en el VoF. Lo que significa que "v" pertenece a S⊥, pero si vos hallas los vectores de S⊥ , el vector "v" no pertenece al mismo y la propiedad dada en el practico de proyeccion dice que  Ps(v)=0 para todo "v" perteneciente a S⊥.

-la segunda es porque cuando vos vas a proyectar un vector sobre S necesitas que la base tenga que ser ortogonal y la que te da en la letra del ejercicio no lo es, y como es una afirmacion deberia de ser falsa. Para que sea verdadera S deberia ser de entrada ortogonal .


En respuesta a Valentin Albornoz Zipitria

Re: Duda ej. de 2do parcial

de Nahuel Alvez Olivera -
Hola, sino me equivoco para que un vector v, en este caso v = (-3,1,3,1,-1), pertenezca a S⊥ basta con que sea ortogonal a cada elemento de una base de S (una base cualquiera de S). En este caso se verifica eso. Y como ya habias dicho vos la proyección ortogonal de v sobre S es el vector nulo, si v pertenece a S⊥. Por lo tanto la proposición es verdadera.
Saludos
En respuesta a Nahuel Alvez Olivera

Re: Duda ej. de 2do parcial

de Mariana Pereira -
Hola,
Venías bien con que Ps(v)=0 v está en S┴
Pero después no sé por qué concluíste que v no estaba en S┴.
Como te dice Nahuel, el vector v=(-3,1,3,1,-1) es ortogonal a cada elemento de la base de S:
<(-3,1,3,1,-1), (1,1,0,2,0)>= -3+1+2=0
<(-3,1,3,1,-1), (0,2,-1,1,0)>= 2-3+1=0
<(-3,1,3,1,-1),(0,0,0,1,1)>= 1-1=0

Sobre la segunda justificación: La proyección es sobre un subespacio S, y el subespacio S puede estar definido o por un conjunto generador, o por una base, o por condiciones que tengan que cumplir los vectores. Para descibir un subespacio no es necesario descibirlo dando una base ortonormal. Y tampoco es necesario tener una base ortonormal para proyectar sobre S, En el único caso en que necesitás tener una BON de S es si para hallar Ps(v) vas a utilizar una fórmula que sea válida solo para BONS. Por ejemplo, hay una fórmula que te dice que si {s1, ..., sk} es una BON de S entonces Ps(v)= s1 + ...+ sk; si se va a utilizar esa fórmula entonces sí tendrías que hallar una BON de S; pero no es la única forma de hallar Ps(v); en particular en la definición de Ps(v) no intervienen las BOS:
DEF: Ps(v) es el único vector de S tal que v-Ps(v) está en S┴

Saludos
En respuesta a Mariana Pereira

Re: Duda ej. de 2do parcial

de Florencia Mikaela Martinez Scheiber -

Ejercicio 2do parcial

Buenas profe

No entiendo como encarar este ejercicio sin hallar una BON de S.

Comencé por hallar una BON de S y me dieron vectores horribles, y no puede llegar a ninguna respuesta. 

En el practico no recuerdo haber hecho ejercicios de proyección ortogonal sin antes ortonormalizar el subespacio.

Gracias.

En respuesta a Florencia Mikaela Martinez Scheiber

Re: Duda ej. de 2do parcial

de Mariana Pereira -
Hola,

Varias cosas:
  1.   No necesitás hallar la proyección ortogonal para contestar la pregunta; basta con ver si lo que te dan, es o no la proyección., es decir, si lo que tan verifica o no la definición de proyección ortogonal del vector. Acordate que PS (v) es el único vector de V que cumple que   P_S(v) \in S \text{ y } v-P_S(v) \in S^{\perp}
  2.  Si querías hallar la proyección ortogonal usando una BON, antes observá que S={ (x, y, z, 0, 0) ; x,y, z, en R} por lo que los primeros 3 vectores de la base canónica forman una bon de S
  3.  Otra cosa que te podía servir era si te dabas cuenta que (0,3,2,0,0) está en S (lo obtenés sumando los 2 primeros generadores de S). y  para todo s en S, PS (s) = s.
  4.  En el video #16 de mis clases (están en el foro de material de clases de zoom) podés ver algunos ejemplosde cómo hallar P_S(v) sin hallar una bon de S

Saludos

Marianita
En respuesta a Mariana Pereira

Re: Duda ej. de 2do parcial

de Florencia Mikaela Martinez Scheiber -
Gracias profeee!!!