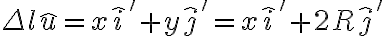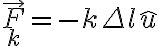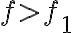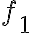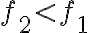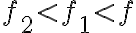Segundo parcial 2010, ejercicio 1

Segundo parcial 2010, ejercicio 1

de Ivan Pablo Martinez Gamba -
Número de respuestas: 2

Buenas, al hacer este ejercicio y ver la resolución, me surgieron dos dudas.

La primera es que en la primer parte, plantean el estiramiento del resorte según i' y j', yo puse al estiramiento según un versor colineal al resorte y luego descompuse en i' y j', lo que hice se puede hacer, no?

al ver la parte 2, no me queda claro por qué al llegar que f_2<f_1 se corrobora la hipótesis de rodadura sin deslizamiento.

Si me pudieran aclarar estas dudas, en especial la 2da, les estaría agradecido.

Gracias, saludos!


En respuesta a Ivan Pablo Martinez Gamba

Re: Segundo parcial 2010, ejercicio 1

de Nicolás Casaballe -
Hola, Iván. Estuve mirando el ejercicio y la solución publicada. Se omite el detalle de varios pasos de los cálculos, como el manejo de la geometría, por ejemplo. No es grave, pero personalmente prefiero que aparezcan más detalles. Se usa un sistema de referencia relativo (no inercial) para la primera cardinal, pero no es necesario y se puede usar un sistema inercial. No queda claro cuál es el sistema en cuál se plantea la segunda cardinal; debería ser con respecto a un sistema inercial o el sistema del CM.

* Con respecto al estiramiento del resorte, tu planteo es lo que implícitamente se hace en la solución: el vector colineal al resorte se puede escribir como
\Delta l \hat u = x \hat i' + y \hat j' = x \hat i' + 2R \hat j'
y la fuerza elástica queda
\vec F_k = -k \Delta l \hat u
(etcétera).

* ¿Se te ocurrió alguna idea de cómo demostrar que el disco rueda sin deslizar al principio? ¿Llegaste a algún resultado?
En la primera parte del ejercicio, la letra pide hallar las condiciones para que se mantenga el equilibrio relativo. Esto conduce a una desigualdad de la forma
(i) f > f_1
donde f_1 es una expresión que depende de los parámetros del sistema. En la parte 2, se encuentra una desigualdad semejante para que se cumpla RSD:
(ii) f > f_2
En la parte 2 ejercicio la letra dice que "En las condiciones de la parte anterior, se corta el resorte" (el evento de cortar el resorte tiene una duración despreciable). Eso significa que, al menos en un entorno de ese momento, se cumple la condición (i). Entonces, dado que f_2 < f_1, usando (i) podemos afirmar que
f_2 < f_1 < f
lo cual implica la condición (ii).

¿Se entiende la explicación? No dudes en consultar de nuevo si hace falta.
Saludos,
NC