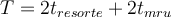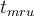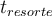Practico 13 - Ejercicio 4

Practico 13 - Ejercicio 4

de Joel Cabrera Dechia -
Número de respuestas: 5

Buenas.

Desde ya pido disculpas si estoy muy denso preguntando por este practico, pero se que es un tema importante y no quiero que se me pase nada.

Yo encaré este ejercicio primero declarando el origen en el punto medio de los resortes y utilicé energía para ver hasta dónde se estira el resorte y así calcular la amplitud. Luego use las condiciones iniciales para hallar w y así calcular el periodo. Pero me dijeron que la respuesta no era esa y la verdad que no entiendo por qué. ¿Es incorrecto aplicar energía en este caso o está mal aplicada?

Adjunto imagen del razonamiento.

Saludos.


En respuesta a Joel Cabrera Dechia

Re: Practico 13 - Ejercicio 4

de Juan Young -

Joel, vos manso, preguntá que para eso estamos.

El tema es así con este ejercicio: El período lo hallás sumando el tiempo que tarda en comprimirse y descomprimirse el resorte una vez, luego lo que tarda la partícula en llegar al otro lado, más el tiempo que tarda en comprimirse y descomprimirse el resorte de nuevo, y luego lo que tarda nuevamente la partícula en llegar el otro lado.

Por lo tanto: T = 2t_{resorte}+2t_{mru}.

El t_{mru} lo hallás rapidito con los conocimientos de cinemática que estoy seguro que tenés.

El t_{resorte} lo hallás recordando como era la frecuencia angular de un sistema masa resorte, y luego recordando cual era la formula del período. Ahora ¿una compresión y descompresión del resorte va a ser un período entero de un sistema masa resorte? ¿O va a ser más? ¿O menos? Esa parte te la dejo a vos. Si no te sale cualquier cosa volvé a preguntar.
En respuesta a Juan Young

Re: Practico 13 - Ejercicio 4

de Joel Cabrera Dechia -
Hola.
Gracias por responder. Lo estuve pensando y concluí que va a ser mayor, mas específicamente el doble, pero la verdad no sabría como justificarlo correctamente (lo pensé como que un periodo es cuando se comprime y al descomprimirse seria otro del mismo valor, por eso el doble).
Llegué a la respuesta correcta, pero tampoco me queda claro por qué no podría haberlo hecho con energía, hallando la amplitud y aplicando las condiciones iniciales.
Saludos.
En respuesta a Joel Cabrera Dechia

Re: Practico 13 - Ejercicio 4

de Joel Cabrera Dechia -
Pará, porque lo del periodo me sigue haciendo ruido, creo que es la mitad.
El periodo es cuánto demora en llegar a un mismo punto, ¿verdad? Entonces, al comprimirse, el resorte va a descomprimirse por la fuerza elástica pero al ser un resorte no va a volver a la longitud natural, sino que va a seguir hasta la amplitud máxima y después volver. Por ejemplo, si supongo que el disco está pegado al resorte, un periodo completo seria cuando se comprime, se descomprime hasta la amplitud máxima y vuelve al punto de longitud natural. Pero al no estar pegado, seria la mitad del periodo.
¿Está bien o es cualca?
En respuesta a Joel Cabrera Dechia

Re: Practico 13 - Ejercicio 4

de Carla Yelpo -
Hola, Joel

La última interpretación que hiciste para determinar el tiempo que demora en comprimirse y descomprimirse el resorte es correcta: ese tiempo será la mitad del período de un sistema masa-resorte.

Respecto a la pregunta de por qué no funciona lo primero que mandaste:

Es cierto que en este sistema se conserva la energía, y que podés usar eso para determinar cuánto se comprimirá el resorte. El error está después, al usar esa información en una ecuación de la forma x(t) = A cos(ωt) para determinar ω.

Esto último no funciona, porque el sistema no va a seguir un movimiento armónico simple. Sí va a ser un movimiento periódico, pero no va a seguir una ecuación de movimiento como la que vimos en el sistema masa-resorte sencillo. Esto es porque, a diferencia de ese sistema, acá no está actuando la fuerza elástica en todo momento. ¿Se entiende? Por eso hace falta separarlo de a tramos, como te sugirió Juan Diego.

Cualquier cosa, volvé a preguntar.

¡Saludos!