Hola, no se interpretar este ejercicio, ¿Podrían darme un pique o algo? porque no llego a la solución.
El 1.76 sale de hacer pitágoras, y el x4 es porque son equistantes. Gracias :D
A mí me está complicando el cálculo de la energía interna. No sé cómo es el planteo, agradezco una ayuda.
Para determinar la energía interna, la idea es que usen la definición que les dan en la nota al final del ejercicio. Lo que debemos calcular es la energía cinética del sistema respecto al centro de masas.
Fijate si con eso sale, y cualquier cosa volvé a preguntar.
¡Saludos!
¿Lograste llegar al resultado? Lo que estás planteando está bien, si querés podés compartirnos lo que hiciste y te ayudamos a encontrar el error.
¡Saludos!
Veo que estás tratando de usar la fórmula Lo = Ioω para determinar el momento angular del sistema. Esa ecuación es válida para un cuerpo rígido con simetría de revolución y que gira alrededor de su eje de simetría. Ese no es el caso del sistema de este problema.
Calculé el momento de cada partícula con la definición: L= ||r||.||p||.sen(θ)

Hola, Brenda
El error está en los ángulos que consideraste que forman los vectores 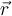 y
y 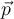 . Fijate que cuando calculás las velocidades respecto a un sistema que se mueve con el centro de masas, las direcciones de esos vectores
velocidad no son las mismas que en el sistema fijo que nos muestran en la figura del ejercicio.
. Fijate que cuando calculás las velocidades respecto a un sistema que se mueve con el centro de masas, las direcciones de esos vectores
velocidad no son las mismas que en el sistema fijo que nos muestran en la figura del ejercicio.
Por ejemplo, vos determinaste (correctamente) que la velocidad de la partícula 1 respecto al centro de masas tiene componentes tanto en 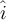 como en
como en 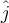 , mientras que la
velocidad que nos muestran en la figura del ejercicio respecto a un sistema fijo sólo tiene componente según
, mientras que la
velocidad que nos muestran en la figura del ejercicio respecto a un sistema fijo sólo tiene componente según 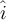 .
.
Para resolver el ejercicio, puede resultar más conveniente pensarlo en componentes. Es decir, escribir la posición de cada partícula respecto al centro
de masas y la velocidad de cada partícula respecto al centro de masas según sus componentes 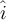 y
y 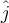 , y luego plantear el producto vectorial haciendo distributiva.
, y luego plantear el producto vectorial haciendo distributiva.
Fijate si por este lado sale. Cualquier cosa, volvé a preguntar.
¡Saludos!