Hola, Belén. Está perfecto que preguntes: de eso se trata el curso! :-)
* La barra experimenta la acción de su propio peso, la reacción correspondiente a su interacción con el disco apoyado sobre esta (fricción y normal) y, además, hay un momento externo aplicado llamado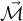 .
.
* La barra experimenta la acción de su propio peso, la reacción correspondiente a su interacción con el disco apoyado sobre esta (fricción y normal) y, además, hay un momento externo aplicado llamado
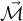 .
. El vector de este momento es perpendicular al plano del dibujo. Por eso la letra dice que es horizontal y ortogonal a la barra. Es una redacción alternativa: sin mencionar el dibujo, hay que decir las dos cosas para que la dirección quede bien definida.
Un defecto de la letra es que no indica el momento respecto a qué punto se considera. Por falta de un mejor candidato, consideramos que es respecto al punto fijo O. Otro detalle faltante es que no se sabe el detalle de las fuerzas externas que producen el momento externo pero, por lo menos para la barra, podemos contestar la pregunta planteando solamente la segunda cardinal.
* La posición del disco en el plano queda determinada por la coordenada 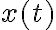 , que ubica su centro con respecto al punto O, junto con cierto ángulo de rotación
, que ubica su centro con respecto al punto O, junto con cierto ángulo de rotación  . No se necesita una coordenada adicional para el centro debido al vínculo de que el disco está apoyado en la barra; sería redundante indicar un
. No se necesita una coordenada adicional para el centro debido al vínculo de que el disco está apoyado en la barra; sería redundante indicar un 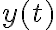 , digamos. El sistema tiene dos grados de libertad. Observa que el centro del disco siempre está a distancia R del punto de contacto.
, digamos. El sistema tiene dos grados de libertad. Observa que el centro del disco siempre está a distancia R del punto de contacto.
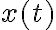 , que ubica su centro con respecto al punto O, junto con cierto ángulo de rotación
, que ubica su centro con respecto al punto O, junto con cierto ángulo de rotación  . No se necesita una coordenada adicional para el centro debido al vínculo de que el disco está apoyado en la barra; sería redundante indicar un
. No se necesita una coordenada adicional para el centro debido al vínculo de que el disco está apoyado en la barra; sería redundante indicar un 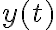 , digamos. El sistema tiene dos grados de libertad. Observa que el centro del disco siempre está a distancia R del punto de contacto.
, digamos. El sistema tiene dos grados de libertad. Observa que el centro del disco siempre está a distancia R del punto de contacto.Por otro lado, como el disco rueda sin deslizar, las coordenadas  y
y 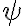 están vinculadas, de manera que al final el número de grados de libertad efectivos es solamente uno. La dinámica del sistema se puede describir con una única ecuación de movimiento para
están vinculadas, de manera que al final el número de grados de libertad efectivos es solamente uno. La dinámica del sistema se puede describir con una única ecuación de movimiento para 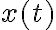 , junto con las ecuaciones de vínculo.
, junto con las ecuaciones de vínculo.
 y
y 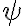 están vinculadas, de manera que al final el número de grados de libertad efectivos es solamente uno. La dinámica del sistema se puede describir con una única ecuación de movimiento para
están vinculadas, de manera que al final el número de grados de libertad efectivos es solamente uno. La dinámica del sistema se puede describir con una única ecuación de movimiento para 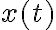 , junto con las ecuaciones de vínculo.
, junto con las ecuaciones de vínculo.---
Espero haber ayudado a aclarar el panorama, pero no dudes en consultar de nuevo cuando quieras.
Saludos,
NC
