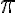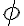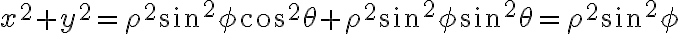MecNew: Duda sobre el cálculo del tensor de inercia para una esfera maciza

Buenas, en el ejercicio 3 se trabaja con una esfera, y en un momento necesito calcular el momento de inercia respecto al eje k (perpendicular al plano) y al punto G (centro de masa).

Para hacer la integral sobre el volumen, cambie X=rcos(phi)sen(theta), Y=rsen(phi)sen(theta), Z=rcos(theta).

Integré r entre (0,R), theta entre (0, pi) y phi entre (0, 2pi). Haciendo esto, llego a que por poner theta entre (0, pi) esa integral me queda 0, pero si cambio los extremos, o sea; Theta entre (0, 2pi), phi entre (0, pi), ahí logro llegar al valor del momento de inercia.

No comprendo por qué al cambiar los extremos obtengo resultados distintos, siendo que para ambos, recorro una vez la esfera, de forma biyectiva.

Pd: perdón por escribir así, no se usar bien las fórmulas que proporciona eva.

Gracias, saludos!

Re: Duda sobre el cálculo del tensor de inercia para una esfera maciza

de Nicolás Casaballe - viernes, 4 de junio de 2021, 20:33

Hola, Ivan. No te preocupes por las fórmulas. Lo importante es que se entienda, y ya vas a tener tiempo para aprender eso más adelante si lo precisas. También está la opción de cargar fotos de lo que escribes a mano, si quieres.

Lo que está sucediendo es que el intervalo correcto de los ángulos es el segundo que elegiste. En coordenadas esféricas uno de los ángulos se limita a un intervalo de tamaño $\pi$ , porque si no habría más de una terna de coordenadas correspondiente al mismo punto del espacio. En la convención que estás utilizando, el ángulo $\phi$ indica el ángulo entre el eje z y el vector de posición del punto, y es el que se restringe entre $0$ y $\pi$ (enlace).

---

No olvides que el cambio de coordenadas cartesianas a esféricas dentro de la integral introduce también un factor en el diferencial de volumen:

$dx\,dy\,dz = r^2 \sin \theta dr \, d\theta \,d\phi$

(debido al determinante del jacobiano de la transformación; más detalles en este enlace).

Por otra parte, no olvidemos que la función que se integra es la distancia al eje z, dada por

$x^2+y ^2 = \rho^2 \sin^2 \phi \cos^2 \theta + \rho^2 \sin^2 \phi \sin^2 \theta = \rho^2 \sin^2 \phi$ .

Entonces vemos que la distancia al eje z no depende del ángulo $\theta$ . Esto es consecuencia de la simetría de revolución alrededor de ese eje. Observemos que si uno prefiere utilizar una convención diferente de coordenadas, es probable que resulte más sencillo calcular otro de los elementos del tensor de inercia... pero finalmente vamos a llegar a que los tres elementos no nulos son iguales, por simetría.

----

Un último comentario: es fascinante saber hacer integrales 3d, pero no es de los temas más relevantes para poder resolver lo ejercicios de nuestro curso. Pienso que con entender adecuadamente la formulación y conocer alguno ejemplos clave es suficiente para nuestros propósitos (por ahora).

Saludos,