Buenas,
Tome un camino ligeramente diferente al del video de la resolucion de este ejercicio, y estoy llegando a una respuesta al impulso que parece ser totalmente distinta. No entiendo por que.
Hice lo siguiente:
Entiendo la resolucion del video y esta re bien explicada. No entiendo donde me estoy equivocando.
Gracias de antemano.

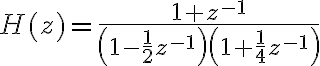
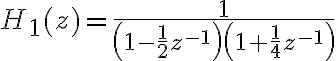
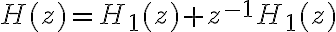
![x[n-n_{0}] \rightarrow z^{-n_{0}}X(z) x[n-n_{0}] \rightarrow z^{-n_{0}}X(z)](https://eva.fing.edu.uy/filter/tex/pix.php/5976ae5a9ca51a3398a33792e703dff2.gif)
![h_{1}[n] h_{1}[n]](https://eva.fing.edu.uy/filter/tex/pix.php/56971828513b1abf89e68ce49770026f.gif)
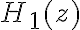
![h[n] h[n]](https://eva.fing.edu.uy/filter/tex/pix.php/76df30cb2f3c2675e057e25429917f27.gif)
![h[n] = h_{1}[n] + h_{1}[n-1] h[n] = h_{1}[n] + h_{1}[n-1]](https://eva.fing.edu.uy/filter/tex/pix.php/fe6e6ebff11237b850e90cc3679ca513.gif)
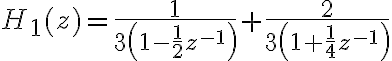
![h_{1}[n] = \frac{1}{3}\left(\frac{1}{2}\right)^{n}u[n] + \frac{2}{3}\left(\frac{-1}{4}\right)^{n}u[n] h_{1}[n] = \frac{1}{3}\left(\frac{1}{2}\right)^{n}u[n] + \frac{2}{3}\left(\frac{-1}{4}\right)^{n}u[n]](https://eva.fing.edu.uy/filter/tex/pix.php/6979757bd937e5cb3c60033c10a3134d.gif)
![h[n] = \frac{1}{3}\left(\frac{1}{2}\right)^{n}u[n] + \frac{2}{3}\left(\frac{-1}{4}\right)^{n}u[n] +\frac{1}{3}\left(\frac{1}{2}\right)^{n-1}u[n-1] + \frac{2}{3}\left(\frac{-1}{4}\right)^{n-1}u[n-1] h[n] = \frac{1}{3}\left(\frac{1}{2}\right)^{n}u[n] + \frac{2}{3}\left(\frac{-1}{4}\right)^{n}u[n] +\frac{1}{3}\left(\frac{1}{2}\right)^{n-1}u[n-1] + \frac{2}{3}\left(\frac{-1}{4}\right)^{n-1}u[n-1]](https://eva.fing.edu.uy/filter/tex/pix.php/aea87c086e4ed3b23a15357a866136e4.gif)