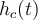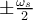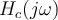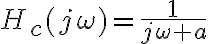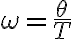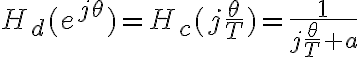Hola,
No estoy seguro del proceso que tengo que hacer para llegar a la respuesta en frecuencia del filtro discreto.
En este ejercicio hay un filtro 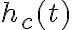 y sus muestras
y sus muestras ![h_{d}[n] = Th_{c}(nT) h_{d}[n] = Th_{c}(nT)](https://eva.fing.edu.uy/filter/tex/pix.php/1f32122cbbd0372355eb5f46a5275557.gif) tomadas a frecuencia
tomadas a frecuencia 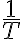
Segun entiendo del teórico, para obtener ![h_{d}[n] h_{d}[n]](https://eva.fing.edu.uy/filter/tex/pix.php/7b4c88ec4a37e6623ac39e76a3bb39d1.gif) tengo que:
tengo que:
- Enventanar
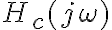 entre
entre 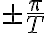 para no tener solapamiento en
para no tener solapamiento en 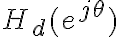 , ya que
, ya que 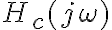 es de soporte no acotado.
es de soporte no acotado. - Muestrear
 , de forma de obtener
, de forma de obtener ![h_{d}[n] = \widetilde{h}_{c}(nT) h_{d}[n] = \widetilde{h}_{c}(nT)](https://eva.fing.edu.uy/filter/tex/pix.php/1a483bf58c8475d8b492833c0acfbe5f.gif)
![h_{d}[n] h_{d}[n]](https://eva.fing.edu.uy/filter/tex/pix.php/7b4c88ec4a37e6623ac39e76a3bb39d1.gif) que yo pienso que estan bien son distintas a las muestras
que yo pienso que estan bien son distintas a las muestras ![h_{d}[n] h_{d}[n]](https://eva.fing.edu.uy/filter/tex/pix.php/7b4c88ec4a37e6623ac39e76a3bb39d1.gif) que me da la letra. Que paso?
que me da la letra. Que paso?Sin embargo, creo que lo importante de este ejercicio es que enventanando 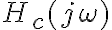 entre
entre 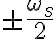 puedo llegar a la expresion de
puedo llegar a la expresion de 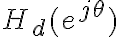 .
.
No estoy logrando llegar a la expresion de 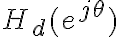 que esta en la solucion. En el teorico vimos que
que esta en la solucion. En el teorico vimos que  . Teniendo la expresion de
. Teniendo la expresion de 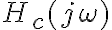 y la relacion anterior , lo que hice fue tomar
y la relacion anterior , lo que hice fue tomar 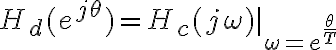 .
.
Esta bien el ultimo cambio de variable? Esa deberia ser la respuesta en frecuencia del filtro discreto?

![h_{d}[n] h_{d}[n]](https://eva.fing.edu.uy/filter/tex/pix.php/7b4c88ec4a37e6623ac39e76a3bb39d1.png)