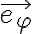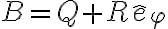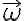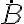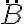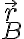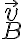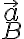Buenas, hice este ejercicio hallando vB con distribución de velocidades, obteniendo el mismo resultado que en las diapositivas de la clase de práctico donde lo presentaron. El problema es que para conseguir aB derivé vB, y me dio distinto a lo que debería; los términos según los versores er y k están iguales, pero en efi tengo
2R(fi 2 puntos - fi punto cuadrado), cuando en la solución son 4 fi punto cuadrado. No logro encontrar el error, ¿es correcta esta forma de hallar la aceleración?
Saludos y gracias.