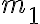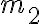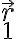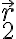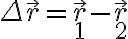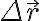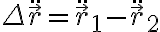Foro Práctico V

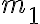
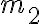
Hola, la idea es que si tenés un sistema de dos partículas, una de masa $m_1$ y otra $m_2$, las cuales solo interactúan ente sí con fuerzas de acción y reacción. Entonces podés hacer un cambio de sistema de referencia.
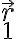
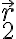
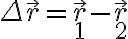
Si respecto al sistema de referencia centrado en el centro de masas las posiciones son $\vec{r}_1$ y $\vec{r}_2$, moves el sistema de referencia a una de las masas, la cual pasa a estar en el origen y la otra pasa a la coordenada $\Delta \vec{r}=\vec{r}_1-\vec{r}_2$ (o al revéz según cual elegiste de origen, no importa realmente). 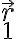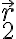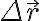Haciendo esto, tu problema que originalmente dependía de dos variables $\vec{r}_1$ y $\vec{r}_2$ ahora solo depende de $\Delta \vec{r}$, la distancia entre las masas.

Entonces:
$\Delta \ddot{\vec{r}}=\ddot{\vec{r}}_1-\ddot{\vec{r}}_2$

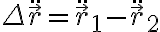
Y sustituyendo en esta ecuación la segunda ley de Newton llegas a la expresión para la masa reducida.

Esto es útil en sistemas de partículas en los que las únicas fuerzas son de interacción porqué se tiene un solo objeto en vez de dos para estudiar. Al hacer esto se puede analizar como se mueve un objeto respecto al otro, pero te olvidas de como se mueven respecto al centro de masas.
En el caso de dos partículas aisladas suele ser más util analizarlo así porque conoces la distancia entre ellas y suele ser lo más importante.

Saludos.