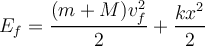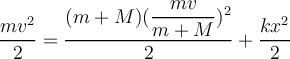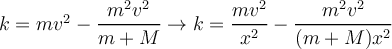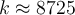Ejercicio 9

Ejercicio 9

de Sofía Dogliotti López -
Número de respuestas: 12

Hola, estoy tratando de hacer el ejercicio 9 y no se bien como encararlo, me podrían dar alguna ayuda? gracias

En respuesta a Sofía Dogliotti López

Re: Ejercicio 9

de Franco Mateo Vienni Baptista -
Buenas Sofia,

Recordar que la masa choca contra el resorte así que el choque es elástico.

p_i=mv
p_f=(m+M)v_f

v_f=\dfrac{mv}{m+M}

Ahora con energía:
E_i=\dfrac{mv^2}{2}

E_f=\dfrac{(m+M)v_f^2}{2} + \dfrac{kx^2}{2}

\dfrac{mv^2}{2} = \dfrac{(m+M)(\dfrac{mv}{m+M})^2}{2} + \dfrac{kx^2}{2}

mv^2 = \dfrac{m^2v^2}{m+M} + kx^2 \rightarrow \boxed{kx^2= m(v^2 - \dfrac{mv^2}{m+M})}

Para la segunda parte:

Si la compresión del resorte es de 0.95 cm, ¿Cuál es la constante del resorte?

k= mv^2 - \dfrac{m^2v^2}{m+M} \rightarrow k= \dfrac{mv^2}{x^2} - \dfrac{m^2v^2}{(m+M)x^2}

Remplazando con los datos del ejercicio se tiene:

k\approx 8725

Saludos,
Franco.
En respuesta a Franco Mateo Vienni Baptista

Re: Ejercicio 9

de Sofía Dogliotti López -
Muchas gracias
En respuesta a Sofía Dogliotti López

Re: Ejercicio 9

de Agustina Maia Laborde Boyrie -

Hola, yo lo que no entiendo del ejercicio es por qué dice que choca inelasticamente cuando en realidad se trata de un resorte, es un error de letra o tiene alguna explicacion? Gracias

En respuesta a Agustina Maia Laborde Boyrie

Re: Ejercicio 9

de Franco Mateo Vienni Baptista -
Buenas Agustina,

El choque al comienzo es elástico ya que la masa choca contra el resorte, pero ni bien se termina de accionar el resorte hasta su compresión máxima el mecanismo se activa y captura a la masa, por lo que ambos cuerpos pasan a moverse juntos como si hubiese ocurrido un choque inelástico.

Saludos,
Franco.
En respuesta a Franco Mateo Vienni Baptista

Re: Ejercicio 9

de Agustina Maia Laborde Boyrie -
Aaaah bien ahora me quedo mucho más claro. Gracias!! Saludos
En respuesta a Agustina Maia Laborde Boyrie

Re: Ejercicio 9

de Carla Yelpo -
Hola, Agustina y Franco

Quisiera hacer una aclaración respecto a la discusión sobre si este choque es elástico o inelástico.

Definimos un choque elástico como aquel en el que se conserva la energía cinética total del sistema. En este caso, eso no se cumple: la energía cinética final no es igual a la inicial.

Lo que sí podemos asegurar es que se conserva la energía mecánica total del sistema, que en este caso es la energía cinética más la energía potencial elástica. ¿Se dan cuenta cómo probar que se cumple esto?

¡Saludos!

En respuesta a Carla Yelpo

Re: Ejercicio 9

de Franco Mateo Vienni Baptista -
Buenas Carla,

¿Basta con el argumento de que la energía cinética perdida queda almacenada en el resorte comprimido? ¿O la pregunta busca una demostración del ámbito matemático?

Saludos,
Franco.
En respuesta a Franco Mateo Vienni Baptista

Re: Ejercicio 9

de Carla Yelpo -
Hola, Franco

Para probarlo, alcanza con verificar que el trabajo de las fuerzas no conservativas es nulo. Analizando las fuerzas externas que actúan sobre este sistema, podemos comprobar que eso es así y por lo tanto se conserva la energía mecánica total del sistema.

¡Saludos!
En respuesta a Carla Yelpo

Re: Ejercicio 9

de Zoé Castro Brando -
Buenas, estaba leyendo la discusión del problema y me surgió la siguiente duda. Entiendo que al no haber fuerzas no conservativas la energía mecánica del sistema se conserva. Ahora bien, si el choque es inelástico, es decir parte de la energía cinética se transforma en interna, aquí la Em no sería no conservativa? Porque la energía interna nunca la consideramos como fuerza conservativa. Sería incorrecto afirmar que, por ejemplo, la energía cinética inicial es igual a la final en un choque inelástico, pues sí sigue habiendo velocidad pero esta se reduce porque parte la absorbe el sistema luego del choque no?
Espero que se haya entendido la duda, espero respuestas.

Saludos.
En respuesta a Zoé Castro Brando

Re: Ejercicio 9

de Alejandro Silva -
Buenas tardes Zoé,

Paso a comentarte, en una colisión inelástica, parte de la energía cinética se pierde en forma de calor, sonido u otras formas de energía interna. A diferencia de un choque elástico, donde los objetos rebotan sin deformarse y conservan la energía cinética total, en un choque inelástico, la energía cinética total no se conserva.

Es decir, en un choque inelástico, la energía mecánica no se conserva, porque se transforma en otros tipos de energía que nosotros no estudiamos en el curso.

Espero que la explicación te haya ayudado, cualquier consulta pregunta nuevamente.

Saludos,
A. Silva
En respuesta a Franco Mateo Vienni Baptista

Re: Ejercicio 9

de Zoé Castro Brando -
Un par de dudas sobre la resolución
1- No faltaría un signo de menos delante de el potencial elástico?
2- Por qué podes anular el dos de denominador en la parte a? Entiendo que matemáticamente es posible, pero lo que te interesa no es despejar la fórmula del potencial elástico tal cual como es? Sino dará un resultado que no se corresponde a la energía potencial absorbida por el elástico, sino al doble de la misma.


En respuesta a Zoé Castro Brando

Re: Ejercicio 9

de Alejandro Silva -
Buenas tardes Zoé,

1- No faltaría un signo de menos delante de el potencial elástico?

Por si recuerdas, el trabajo del potencial elástico era negativo (ya que la fuerza siempre se opone al vector \vec{\Delta x} ), y por como definimos el potencial, como el opuesto del trabajo, resulta que la energía potencial elástica es positiva. Podés pensarlo como que se "guarda" energía en el resorte.

2- Por qué podes anular el dos de denominador en la parte a? 

Para hallar el valor de la energía potencial elástica tenemos que tener en cuenta el un medio, tenés razón.


Espero haberte ayudado, cualquier consulta pregunta nuevamente.

Saludos,
A. Silva