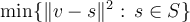Foro de dudas del práctico 6

Hola a los dos,

La idea es usar que entre todos los vectores s de S, P_S (v) es el que "está más cerca de v". En el sentido que el valor mínimo de 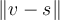$\| v-s \|$ se obtiene cuando s= P_S (v) (esto se deduce del Teorema 134 del libro).

Entonces, para un v fijo, 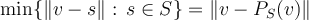$\text{min} \{\| v-s\|: \, s\in S\} = \| v-P_S(v)\|$ (y lo mismo para las normas al cuadrado)

La idea del ejercicio es que 

$\text{min} \{ F(a,b,c) : \, (a,b,c) \in \mathbb{R}^3\}$

se puede escribir como  $\text{min} \{\| v-s\|^2: \, s\in S\}$

para algún espacio vectorial con producto interno, S subespacio y v vector fijo.

Pista: Fíjense que si bien la variable de F es (a,b,c) en R^3 (y por eso pide hallar el mínimo de F en R^3), 

en la fórmula de F,  el  (a,b,c) sólo aparece en at² + bt + c. Entonces al variar  (a,b,c) lo que varía es el polinomio at² + bt + c. Y entonces se podría escribir F en función de un polinomio de grado 2.

 Díoganme si con esas pistas lo pueden resolver, si no pueden, ayudo un poco más.

Saludos

Marianita