Hola Serrana,
la proyección ortogonal es sobre el subespacio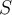 , por lo tanto la solución debe ser un vector del propio
, por lo tanto la solución debe ser un vector del propio 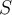 .
.
Además, si razonamos como mencionas lo que estaríamos hallando son las coordenadas del vector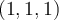 en una base del espacio vectorial
en una base del espacio vectorial  , porque
, porque 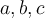 son justamente los coeficientes por los cuales hay que multiplicar a la base para obtener al vector en cuestión. Esto no es la definición de proyección ortogonal.
son justamente los coeficientes por los cuales hay que multiplicar a la base para obtener al vector en cuestión. Esto no es la definición de proyección ortogonal.
Espero aclare tu duda.
Saludos
la proyección ortogonal es sobre el subespacio
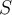 , por lo tanto la solución debe ser un vector del propio
, por lo tanto la solución debe ser un vector del propio 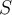 .
.Además, si razonamos como mencionas lo que estaríamos hallando son las coordenadas del vector
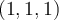 en una base del espacio vectorial
en una base del espacio vectorial  , porque
, porque 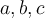 son justamente los coeficientes por los cuales hay que multiplicar a la base para obtener al vector en cuestión. Esto no es la definición de proyección ortogonal.
son justamente los coeficientes por los cuales hay que multiplicar a la base para obtener al vector en cuestión. Esto no es la definición de proyección ortogonal. Espero aclare tu duda.
Saludos