Buenas, en este ejercicio no entendí la referencia del tronco. Donde en que está, si al costado de la canoa, al frente o abajo. Gracias.
La respuesta es que no importa, creo. Lo unico que pretende decir es que es un un punto fijo respecto de la canoa, es decir, inercial.
Yo tengo dudas respecto a la solución que se planteó ayer respecto a las posiciones de cada elemento del sistema.
No me doy cuenta de cuales son las X de Julio y Ricardo al final, después de intercambiar sus lugares.
Se planteó que el desplazamiento de la canoa respecto de ese tronco fue de L, hasta ahí bien.
Pero cuando se planteó las posiciones de ricardo y julia una vez que intecambiaron de lugar, quedaron (d es el largo de la canoa):
X(ricardo) = L + d
X(julia) = L
Etiendo que deberían ser al reves las posiciones, me equivoco? o copie mal tal vez de la solución?
Gracias
Yo tengo dudas respecto a la solución que se planteó ayer respecto a las posiciones de cada elemento del sistema.
No me doy cuenta de cuales son las X de Julio y Ricardo al final, después de intercambiar sus lugares.
Se planteó que el desplazamiento de la canoa respecto de ese tronco fue de L, hasta ahí bien.
Pero cuando se planteó las posiciones de ricardo y julia una vez que intecambiaron de lugar, quedaron (d es el largo de la canoa):
X(ricardo) = L + d
X(julia) = L
Etiendo que deberían ser al reves las posiciones, me equivoco? o copie mal tal vez de la solución?
Gracias
Hola, Alexis
Entiendo que estás usando al notación como lo vimos en la clase del viernes, ¿correcto? En ese caso, L es la distancia entre el origen que nos tomamos como referencia y el extremo de la canoa más próximo a ese origen, y d el largo de la canoa.
Nosotros consideramos que Julia inicialmente se encuentra del lado más próximo al origen y Ricardo del lado más lejos. Teniendo eso en cuenta, las posiciones que escribes allí son las posiciones iniciales de Julia y Ricardo. Las posiciones finales quedaban un poco diferentes (no exactamente al revés) porque tenemos que tener en cuenta que la canoa también se desplaza respecto a nuestro origen.
Fijate si estos comentarios ayudan a entender un poco mejor lo que hicimos en clase. Cualquier cosa, volvé a preguntar.
¡Saludos!
Entiendo que estás usando al notación como lo vimos en la clase del viernes, ¿correcto? En ese caso, L es la distancia entre el origen que nos tomamos como referencia y el extremo de la canoa más próximo a ese origen, y d el largo de la canoa.
Nosotros consideramos que Julia inicialmente se encuentra del lado más próximo al origen y Ricardo del lado más lejos. Teniendo eso en cuenta, las posiciones que escribes allí son las posiciones iniciales de Julia y Ricardo. Las posiciones finales quedaban un poco diferentes (no exactamente al revés) porque tenemos que tener en cuenta que la canoa también se desplaza respecto a nuestro origen.
Fijate si estos comentarios ayudan a entender un poco mejor lo que hicimos en clase. Cualquier cosa, volvé a preguntar.
¡Saludos!
Bien, lo volví a hacer y quedó, muchas gracias!
Buenas, estoy haciendo el ejercicio y no me está saliendo. Subo lo que hice porque se ve que entendí mal tu explicación.
Hola, Juan Manuel
Ojo que la posición que permanece constante es la posición del centro de masas de todo el sistema (Julia + Ricardo + canoa). En tus ecuaciones para la posición del centro de masas, faltó considerar el término correspondiente a la canoa.
Por otra parte, entiendo que faltó considerar el dato de que Julia pesa menos. Teniendo esto en cuenta y que la posición del centro de masas de todo el sistema debe permanecer constante, ¿la canoa se aleja del tronco o se acerca a él?
Fijate si con esto podés resolver. Cualquier cosa, volvé a preguntar.
¡Saludos!
Ojo que la posición que permanece constante es la posición del centro de masas de todo el sistema (Julia + Ricardo + canoa). En tus ecuaciones para la posición del centro de masas, faltó considerar el término correspondiente a la canoa.
Por otra parte, entiendo que faltó considerar el dato de que Julia pesa menos. Teniendo esto en cuenta y que la posición del centro de masas de todo el sistema debe permanecer constante, ¿la canoa se aleja del tronco o se acerca a él?
Fijate si con esto podés resolver. Cualquier cosa, volvé a preguntar.
¡Saludos!
Hola Buenas tardes, Con el tema de la canoa, no entiendo que posición es la que utilizamos para ubicarla, pues es un cuerpo alargado, ¿ que posición debería tener entonces?.
Esta misma duda surge con el ejercicio 4, del perro y el bote, ya que para calcular el centro de masa necesito una posición para el bote, pero no me queda clara cual debería ser. Desde ya muchas gracias.
Esta misma duda surge con el ejercicio 4, del perro y el bote, ya que para calcular el centro de masa necesito una posición para el bote, pero no me queda clara cual debería ser. Desde ya muchas gracias.
Hola, Nicolás
La idea es que consideremos que la masa de la canoa está uniformemente distribuida. Entonces, el centro de masa de la canoa coincidirá con su centro geométrico, es decir, el medio de la canoa. ¿Te das cuenta por qué?
Esa posición es la usamos luego para determinar el centro de masa de todo el sistema.
¿Se entiende la idea? Cualquier cosa volvé a preguntar.
¡Saludos!
Comprendí la idea, y el motivo es que, si consideramos a la canoa, como un conjunto de muchas partículas, al tener todas la misma masa, al hacer el centro de masa, obtenemos el centro Geométrico. Muchas Gracias por su tiempo!
Agrego: Por eso también conviene tomar la posición de la canoa desde ese centro geométrico. Reitero las gracias!
No sé si es correcto el razonamiento, pero creo que la canoa tiende a moverse en sentido contrario a Ricardo. Como posee la mayor masa, el centro de masa debería estar más cerca de él cuando se mueve, entonces para que la posición del CM se mantenga constante, la canoa tiende a deslizarse para "compensar" la posición. No sé si se entendió bien.
Hola, Lorenzo
Tal como dice Alexis, el lugar donde se encuentra ese tronco que tomes como referencia no va a afectar el resultado. Lo importante es que definas un origen fijo desde donde medir todas las distancias que necesites para resolver el problema. Pero el resultado no dependerá de dónde ubicaste ese origen.
¡Saludos!
Tal como dice Alexis, el lugar donde se encuentra ese tronco que tomes como referencia no va a afectar el resultado. Lo importante es que definas un origen fijo desde donde medir todas las distancias que necesites para resolver el problema. Pero el resultado no dependerá de dónde ubicaste ese origen.
¡Saludos!
Medí las distancias desde el tronco, no sé si es correcto, pero no estoy llegando a la solución.
hola, tengo una duda de este ejercicio también, no logro comprender como se pueden mover solo por el hecho de cambiar las masas de lugares, que fuerzas actúan y por que depende de las masas la distancia que se movió? o sea que si sacamos las masas, de alguna forma sin tocar el bote, que sucede con la posición del bote? y si le agregamos mas masa de un lado? se movería al lado contrario? o hacia el lado que haya mas masa? y una vez que se mueve que lo frena?
Hola, Pedro
Estás planteando muchas preguntas interesantes, pero creo que para entender la respuesta a cada una de ellas, primero tenemos que preguntarnos cómo se mueve el centro de masas del sistema Ricardo + Julia + canoa.
Tomando ese sistema, las fuerzas externas que actúan sobre él son el peso de cada una de las partes, y la fuerza de empuje que está ejerciendo el agua para que la canoa con Julia y Ricardo adentro se mantenga a flote.
Sabemos que la canoa no se está hundiendo, por lo que podemos afirmar que esas fuerzas externas se anulan entre sí.
Recordando la segunda ley de Newton aplicada a un sistema de partículas, tenemos que la suma de fuerzas externas aplicadas sobre nuestro sistema debe ser igual a la masa total del sistema multiplicada por la aceleración del centro de masas, es decir:
Entonces, si la suma de fuerzas externas es cero, la aceleración del centro de masas también es cero. Por lo tanto, la velocidad del centro de masas debe ser constante. Además, como el sistema está inicialmente en reposo, la velocidad inicial del centro de masas debe ser cero. Y como ésta es constante, entonces debe ser cero en todo momento.
Si la velocidad del centro de masas es cero, entonces la posición del centro de masas debe ser constante. Es decir, el centro de masas debe permanecer siempre en el mismo lugar. Y la razón para esto, por lo que vimos recién, es porque la suma de fuerzas externas es cero y el sistema parte del reposo.
Cuando Ricardo y Julia cambian de lugar, este razonamiento sigue siendo válido. Fijate que para que puedan desplazarse, ellos deben ejercer una fuerza sobre la canoa, pero por la tercera ley de Newton, la canoa ejercerá a su vez, una fuerza sobre ellos. Esas fuerzas son, por lo tanto, fuerzas internas al sistema que se anulan entre sí.
Ahora bien, cuando Ricardo y Julia se mueven, la distribución de masas del sistema se va a ver alterada. El desplazamiento de la canoa debe ser tal que el centro de masas permanezca en el mismo lugar que al principio. Como la posición del centro de masas depende de la masa de las partes del sistema y dónde se encuentran cada una de ellas, cuánto se desplazó la canoa dependerá del valor de las masas de Ricardo, Julia y la canoa (además de sus respectivas posiciones).
En cambio, si "sacamos las masas" de alguna forma, ahí ya no va a ser cierto todo lo que planteamos. Porque para "sacar" las masas de allí, estaremos ejerciendo una fuerza externa sobre el sistema. Lo mismo si le agregamos más masa a la canoa.
Por último, si Ricardo y Julia dejan de moverse, la canoa también deberá dejar de moverse. De lo contrario, el centro de masa del sistema estaría modificando su velocidad (es decir, se estaría acelerando) sin que apliquemos una fuerza externa sobre el mismo.
Espero que esto ayude a entender mejor el problema. Si alguna cosa no quedó clara, volvé a preguntar.
¡Saludos!
Hola gracias por responder, comprendo el por que el centro de masa debe ser constante, pero no comprendo que hace mover al bote para mantener esa constancia, porque mencionas que realizan una fuerza cuando se desplazan, supongo que es la fuerza rozamiento, pero si se anulan entonces la fuerza neta total en todo el intervalo es 0, como se puede mover entonces, entiendo que se tiene que mover ya que el centro de masa no se mueve pero para mover el barco necesitamos una fuerza no? y también hay otra fuerza que lo frena porque después supongo que llega al reposo
Hola Pedro.
Como mencionó Carla, las fuerzas de rozamiento son fuerzas internas del sistema Ricardo + Julia + canoa. La suma de esas fuerzas es cero, pero eso no significa que esas fuerzas no existan. De hecho, la fuerza que cada una de las personas aplica a la canoa al variar su posición, es la que le permite moverse respecto al agua para mantener la velocidad del CM invariante. El hecho de que se conserve la velocidad (y en este caso, también la posición) del CM, no impide que las componentes del sistema se muevan respetando esa conservación y, cuando lo hacen, es a causa de esas fuerzas internas.
Saludos!
Como mencionó Carla, las fuerzas de rozamiento son fuerzas internas del sistema Ricardo + Julia + canoa. La suma de esas fuerzas es cero, pero eso no significa que esas fuerzas no existan. De hecho, la fuerza que cada una de las personas aplica a la canoa al variar su posición, es la que le permite moverse respecto al agua para mantener la velocidad del CM invariante. El hecho de que se conserve la velocidad (y en este caso, también la posición) del CM, no impide que las componentes del sistema se muevan respetando esa conservación y, cuando lo hacen, es a causa de esas fuerzas internas.
Saludos!
Bien gracias a las dos.
Hola, Brenda
El planteo que hiciste es correcto y las posiciones que escribiste para el centro de masa en el estado inicial y final están bien.
Tuviste un error en las cuentas, concretamente en la tercer línea contando desde abajo, cuando sacás las masas m2 y m3 como factor común. En el término con m3, la distancia d debería tener un signo negativo.
Un comentario respecto al dibujo: indicaste como que el centro de masa estaba en el centro del bote, pero en realidad, si mirás la expresión que te quedó para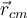 
, esa posición no va a estar en l/2, sino que va a estar un poco corrido. ¿Te das cuenta para qué lado?
¡Saludos!