Hola! Era para preguntar el siguiente ejercicio, a mí me quedaba que para dos valores k1,k2 distintos de b, T era diagonalizable. Me podrían explicar cómo se debía resolver? Ya que eso estaba mal.
Gracias
Hola! Era para preguntar el siguiente ejercicio, a mí me quedaba que para dos valores k1,k2 distintos de b, T era diagonalizable. Me podrían explicar cómo se debía resolver? Ya que eso estaba mal.
Gracias
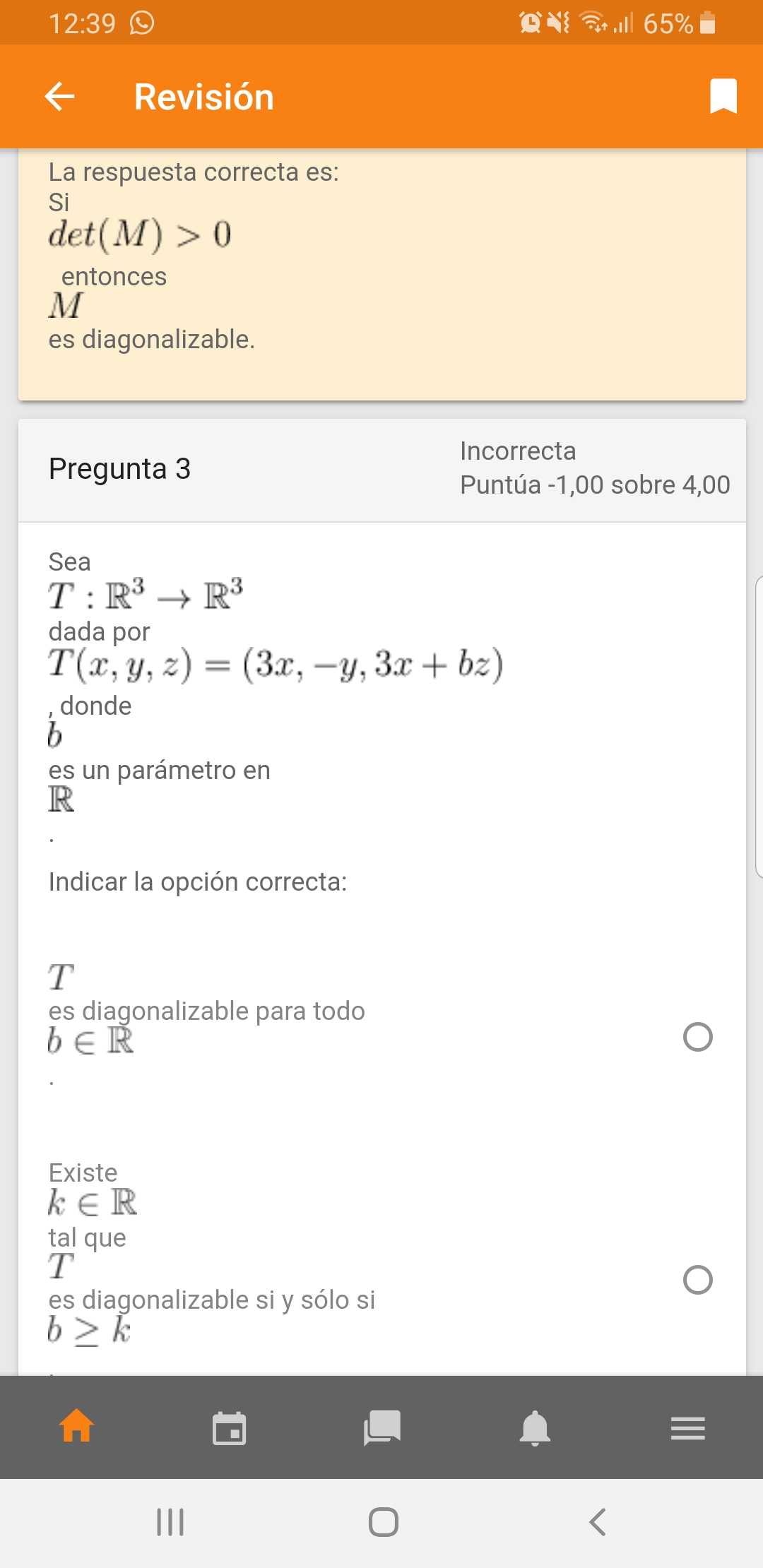
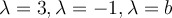 . Por tanto si
. Por tanto si 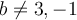 T es diagonalizable pues tendría tres vps distintos. Ahora, si
T es diagonalizable pues tendría tres vps distintos. Ahora, si 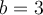 se hace la cuenta y se ve que T no es diagonalizable. Por otro lado para
se hace la cuenta y se ve que T no es diagonalizable. Por otro lado para 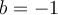 resulta que sí es diagonalizable. En conclusión T es diagonalizable si y solo si
resulta que sí es diagonalizable. En conclusión T es diagonalizable si y solo si 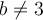 .
.