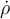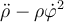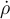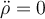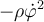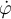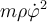MecNew: Ejercicio 1 primer parcial 2015

Buenas, perdón que escriba acá, no se si hay un foro estrictamente para este tipo de dudas.

La letra de este ejercicio dice que se ejerce una fuerza Fr "de modo que la componente radial de la velocidad se mantiene constante durante todo el movimiento". No entiendo por qué la velocidad radial se mantiene constante siendo que existe una fuerza radial, por lo tanto una aceleración radial.

Gracias, saludos!

Re: Ejercicio 1 primer parcial 2015

de Ricardo Marotti - domingo, 2 de mayo de 2021, 18:08

Estimado:

Tenés que fijarte cómo son las componentes de la velocidad y la aceleración en coordenadas cilíndricas. La componente radial de la velocidad es

$\dot{ \rho }$ , y la componente radial de la aceleración es

$\ddot{ \rho } - \rho \dot{ \varphi }^2$ . Si

$\dot{ \rho }$ es constante,

$\ddot{ \rho } = 0$ . O sea que la aceleración radial tendrá todavía la componente centrípeta

$- \rho \dot{ \varphi }^2$ , que multiplicada por la masa será igual a la componente radial de la fuerza.

O sea, que la componente radial de la velocidad sea nula no implica que la aceleración radial sea nula, visto desde un sistema inercial fijo.

Visto de otra forma, si te parás en el sistema de referencia que se mueve con velocidad angular

$\dot{ \varphi }$ , ahí si que la velocidad relativa sea constante quiere decir que la aceleración relativa es cero. Pero habrá una fuerza ficticia centrífuga

$m \rho \dot{ \varphi }^2$ que tiene que oponerse a la fuerza real aplicada.

Saludos:

Ricardo.