Estimada:
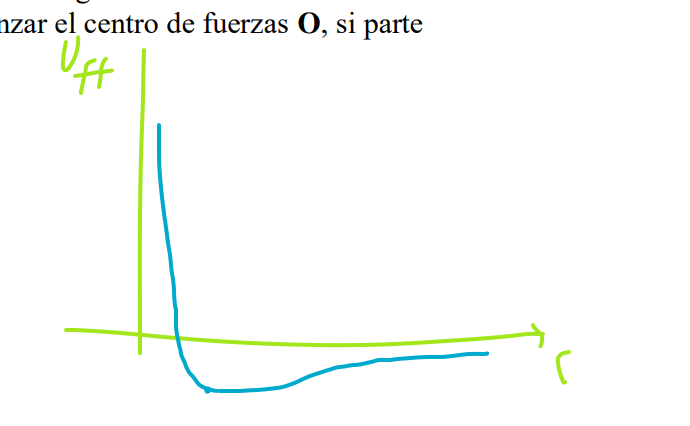
La forma de graficar una energía potencial efectiva es solo eso: graficar una función. Ahí es recordar la información que nos dan los límites en los extremos del entorno en que la función está definida. Eventualmente hallar las derivadas de la función para ver qué extremos relativos tiene, y si se precisan hallar ceros y singularidades de la función. Aunque generalmente lo que queremos es un bosquejo cualitativo de la misma, y no necesariamente calcular la posición de todos estos puntos especiales (salvo que se pida alguna condición particular respecto a alguno de ellos).
Luego que tenemos la gráfica de la energía potencial efectiva, hay que recordar que los extremos relativos de la función nos dan las posiciones de equilibrio: los mínimos son posiciones de equilibrio estables, los máximos son posiciones de equilibrio inestable. En los casos de más de un grado de libertad, como en movimiento central, solo será la coordenada que se está estudiando constante. Ahí, en el caso de movimiento central, en que tenemos una energía potencial efectiva en función de ρ, y
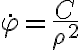
, donde C es una constante, los extremos de la energía potencial efectiva dan lugar a movimientos circulares uniformes (estables o inestables, respectivamente)
Además hay que recordar que si el sistema es conservativo se verifica la conservación de la energía: T + U = E. T es la energía cinética. U la energía potencial efectiva y E la energía mecánica total, que es una constante que depende de las condiciones iniciales. Ahora por definición de energía cinética la misma solo puede ser positiva o cero: T = E - U ≥ 0. O sea que el movimiento es posible solo en la región de la energía potencial efectiva donde E ≥ U. Los puntos en que E = U (que no son extremos relativos de U) son puntos de retroceso en que la velocidad cambia de signo (si
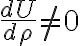
habrá una fuerza
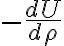
no nula que evitará que ρ sea constante).
Esa es básicamente la información más importante que nos dan esas gráficas.
Saludos:
Ricardo.

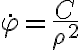 , donde C es una constante, los extremos de la energía potencial efectiva dan lugar a movimientos circulares uniformes (estables o inestables, respectivamente)
, donde C es una constante, los extremos de la energía potencial efectiva dan lugar a movimientos circulares uniformes (estables o inestables, respectivamente)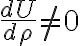 habrá una fuerza
habrá una fuerza 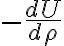 no nula que evitará que ρ sea constante).
no nula que evitará que ρ sea constante).