Estimada:
En tu solución encuentro los siguientes errores.
1) Dice que la fuerza es atractiva, y lo que da la letra es su módulo. O sea que k es positiva. Por lo tanto la proyección según la dirección radial saliente debe ser
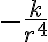. O sea que tenés mal el signo de la fuerza (O tu K es negativa). 2) Antes de preintegrar, cuando pasás el término de la aceleración centrípeta para el otro lado, tiene que cambiar de signo. Efectivamente esto da lugar a la fuerza centrífuga que tiene que ser positiva.
Juntando ambos errores de signo tu 
te quedó cambiado de signo.
te quedó cambiado de signo. 3) Al evaluar la constante el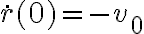 
. No entiendo qué es lo que hiciste vos. Creo que intentaste proyectar la velocidad según la dirección radial y θ es el ángulo entre la velocidad y esa dirección. Pero en todo caso debería ser coseno en lugar de seno. Que cuando la partícula está muy lejos el ángulo es cero y su coseno vale 1. Pero todavía tenés que tener en cuenta el signo. La partícula se acerca al punto O, por lo que r decrece, y su derivada tiene que ser negativa.
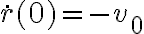. No entiendo qué es lo que hiciste vos. Creo que intentaste proyectar la velocidad según la dirección radial y θ es el ángulo entre la velocidad y esa dirección. Pero en todo caso debería ser coseno en lugar de seno. Que cuando la partícula está muy lejos el ángulo es cero y su coseno vale 1. Pero todavía tenés que tener en cuenta el signo. La partícula se acerca al punto O, por lo que r decrece, y su derivada tiene que ser negativa. Saludos:
Ricardo.